Simpangan Baku Data Tunggal
Hitung Rerata C Hitung Variansi Dan Simpangan Baku D Hitung
Pelajaran, Soal & Rumus Simpangan Baku Data Tunggal
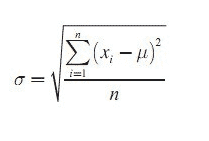
Cari rata-rata terlebih dahulu :
$\begin{aligned}\overline{x} & =\frac{5(2)+6(5)+7(12)+8(7)+9(4)}{2+5+12+7+4}\\ & =\frac{10+30+84+56+36}{30}\\ & =\frac{216}{30}\\ & =7,2 \end{aligned}
$
$S^{2}=\frac{2\left(5-7,2\right)^{2}+5(6-7,2)^{2}+12(7-7,2)^{2}+7(8-7,2)^{2}+4(9-7,2)^{2}}{2+5+12+7+4}$
$\begin{aligned}S^{2} & =\frac{9,68+7,2+0,48+4,48+12,96}{30}\\ & =\frac{34,8}{30}\\ & =1,16 \end{aligned}
$
$\begin{aligned}S & =\sqrt{1,16}\\ & =1,08. \end{aligned}
$
Jadi simpangan bakunya adalah $1,08.$
Cari rata-rata terlebih dahulu :
$\begin{aligned}\overline{x} & =\frac{5(2)+6(5)+7(12)+8(7)+9(4)}{2+5+12+7+4}\\ & =\frac{10+30+84+56+36}{30}\\ & =\frac{216}{30}\\ & =7,2 \end{aligned}
$
$S^{2}=\frac{2\left(5-7,2\right)^{2}+5(6-7,2)^{2}+12(7-7,2)^{2}+7(8-7,2)^{2}+4(9-7,2)^{2}}{2+5+12+7+4}$
$\begin{aligned}S^{2} & =\frac{9,68+7,2+0,48+4,48+12,96}{30}\\ & =\frac{34,8}{30}\\ & =1,16 \end{aligned}
$
$\begin{aligned}S & =\sqrt{1,16}\\ & =1,08. \end{aligned}
$
Jadi simpangan bakunya adalah $1,08.$
$\begin{aligned}S^{2} & =\frac{\sum_{i=1}^{n}\left(x_{i}\right)^{2}}{n}-\left\{ \frac{\sum_{i=1}^{n}x_{i}}{n}\right\} ^{2}\\ & =\frac{131}{5}-\left\{ \frac{25}{5}\right\} ^{2}\\ & =26,2-25\\ & =1,2. \end{aligned}
$
$\begin{aligned}S^{2} & =\frac{\sum_{i=1}^{n}\left(x_{i}\right)^{2}}{n}-\left\{ \frac{\sum_{i=1}^{n}x_{i}}{n}\right\} ^{2}\\ & =\frac{131}{5}-\left\{ \frac{25}{5}\right\} ^{2}\\ & =26,2-25\\ & =1,2. \end{aligned}
$
Diketahui $n$ buah data: $x_{1},\, x_{2},\,…x_{n}.$ dengan $\overline{x}=5,3;\, S=1,9$ dan $Q1=1,6.$ Jika masing-masing data dikalikan $3$ kemudian dikurangi $2,$ maka nilai $\overline{x}$, $S$ dan $Q1$ sekarang adalah…
Jika terjadi perubahan pada setiap data, perubahannya dapat terlihat pada tabel berikut :
Dari data diatas bisa diperoleh :
Rata-rata baru diperoleh $=13,9$
Simpangan baku baru diperoleh $=5,7$
Quartil bawah diperoleh $=2,8.$
Jika terjadi perubahan pada setiap data, perubahannya dapat terlihat pada tabel berikut :
Dari data diatas bisa diperoleh :
Rata-rata baru diperoleh $=13,9$
Simpangan baku baru diperoleh $=5,7$
Quartil bawah diperoleh $=2,8.$
Misalkan data awalnya adalah $x_{1},x_{2},x_{3},…,x_{40}$
$\bar{x}=\frac{x_{1}+x_{2}+x_{3}….+x_{40}}{40}$
Setelah setiap data dikalikan $2$ dan dikurangin $10,$ maka menjadi :
$\frac{2x_{1}-10+2x_{2}-10+2x_{3}-10….+2x_{40}-10}{40}$$=\frac{2(x_{1}+x_{2}+x_{3}….+x_{40})-10.40}{40}$
$=2\overline{x}-10$
$=64-10$
$=54$
Dengan menggunakan alternatif diperoleh :
Jika terjadi perubahan pada setiap data, perubahannya dapat terlihat pada tabel berikut :
Misalkan data awalnya adalah $x_{1},x_{2},x_{3},…,x_{40}$
$\bar{x}=\frac{x_{1}+x_{2}+x_{3}….+x_{40}}{40}$
Setelah setiap data dikalikan $2$ dan dikurangin $10,$ maka menjadi :
$\frac{2x_{1}-10+2x_{2}-10+2x_{3}-10….+2x_{40}-10}{40}$$=\frac{2(x_{1}+x_{2}+x_{3}….+x_{40})-10.40}{40}$
$=2\overline{x}-10$
$=64-10$
$=54$
Dengan menggunakan alternatif diperoleh :
Jika terjadi perubahan pada setiap data, perubahannya dapat terlihat pada tabel berikut :
Jika terjadi perubahan pada setiap data, perubahannya dapat terlihat pada tabel berikut :
Jadi yang memenuhi adalah $C.$
Jika terjadi perubahan pada setiap data, perubahannya dapat terlihat pada tabel berikut :
Jadi yang memenuhi adalah $C.$
Gallery Simpangan Baku Data Tunggal
Statistika Data Tunggal Ragam Varian Simpangan Baku Part 2
Statistika Diagram Tabel Median Modus Kuartil Soal
Simpangan Baku Dari Sekelompok Data Tunggal 7 3 5 4 6 5
007 Seri Statistik Uji Hipotesis Mean Tunggal Dengan
Tutorial Cara Mudah Dan Cepat Menentukan Dan Menghitung Simpangan Baku Data Kelompok
Cara Menghitung Simpangan Baku Beserta Rumus Dan Contoh Soal
Ukuran Penyebaran Data Ppt Download
Dua Cara Hitung Simpangan Baku Data Tunggal Dengan Ms Excel
Simpangan Baku Pembuktian Rumus Cara Menentukan Dan Contoh
I 4 Ragam S B 2 Dan Simpangan Baku S B Ragam Dan Simpangan
Standar Deviasi Pengertian Rumus Dan Contoh Soal Lengkap
Pelajaran Soal Rumus Simpangan Baku Data Tunggal
Pelajaran Soal Rumus Simpangan Baku Data Tunggal
Statistics Of Diversity And Standard Deviation Dat For
Rumus Simpangan Baku Data Tunggal 2942013 My Blog My
Contoh Soal Simpangan Rata Rata Dan Penyelesaiannya
Simpangan Baku
Statistics Of Data Variety And Standard Deviation For
Standar Deviasi Pengertian Rumus Dan Contoh Soal Lengkap
Standar Deviasi Pengertian Rumus Dan Contoh Soal Lengkap
Pembahasan Soal Ragam Simpangan Baku Dan Simpangan Rata
Ukuran Variasi Atau Dispersi Pengukuran Varians Ppt Download
0 Response to "Simpangan Baku Data Tunggal"
Post a Comment