Analisis Regresi Linear Berganda
 Uji Analisis Regresi Linear Ganda Dengan Spss Konsistensi
Uji Analisis Regresi Linear Ganda Dengan Spss Konsistensi
Regresi Linear Berganda

Secara umum regresi linear terdiri dari dua, yaitu regresi linear sederhana yaitu dengan satu buah variabel bebas dan satu buah variabel terikat; dan regresi linear berganda dengan beberapa variabel bebas dan satu buah variabel terikat. Analisis regresi linear merupakan metode statistik yang paling jamak dipergunakan dalam penelitian-penelitian sosial, terutama penelitian ekonomi. Program komputer yang paling banyak digunakan adalah SPSS (Statistical Package For Service Solutions).
Regresi Linear Sederhana
Analisis regresi linear sederhana dipergunakan untuk mengetahui pengaruh antara satu buah variabel bebas terhadap satu buah variabel terikat. Persamaan umumnya adalah:
Y = a + b X.
Dengan Y adalah variabel terikat dan X adalah variabel bebas. Koefisien a adalah konstanta (intercept) yang merupakan titik potong antara garis regresi dengan sumbu Y pada koordinat kartesius.
Langkah penghitungan analisis regresi dengan menggunakan program SPSS adalah: Analyse --> regression --> linear. Pada jendela yang ada, klik variabel terikat lalu klik tanda panah pada kota dependent. Maka variabel tersebut akan masuk ke kotak sebagai variabel dependen. Lakukan dengan cara yang sama untuk variabel bebas (independent). Lalu klik OK dan akan muncul output SPSS.
Interpretasi Output
Nilai t hitung dan signifikansi
Nilai t hitung > t tabel berarti ada pengaruh yang signifikan antara variabel bebas terhadap variabel terikat, atau bisa juga dengan signifikansi di bawah 0,05 untuk penelitian sosial, dan untuk penelitian bursa kadang-kadang digunakan toleransi sampai dengan 0,10.
Sebagai ilustrasi variabel bebas: Biaya promosi dan variabel terikat: Profitabilitas (dalam juta rupiah) dan hasil analisisnya Y = 1,2 + 0,55 X. Berarti interpretasinya:
Jika besarnya biaya promosi meningkat sebesar 1 juta rupiah, maka profitabilitas meningkat sebesar 0,55 juta rupiah.
Jika biaya promosi bernilai nol, maka profitabilitas akan bernilai 1,2 juta rupiah.
Interpretasi terhadap nilai intercept (dalam contoh ini 1,2 juta) harus hati-hati dan sesuai dengan rancangan penelitian. Jika penelitian menggunakan angket dengan skala likert antara 1 sampai 5, maka interpretasi di atas tidak boleh dilakukan karena variabel X tidak mungkin bernilai nol.
Regresi Linear Berganda
Analisis regresi linear berganda sebenarnya sama dengan analisis regresi linear sederhana, hanya variabel bebasnya lebih dari satu buah. Persamaan umumnya adalah:
Y = a + b1 X1 + b2 X2 + .... + bn Xn.
Dengan Y adalah variabel bebas, dan X adalah variabel-variabel bebas, a adalah konstanta (intersept) dan b adalah koefisien regresi pada masing-masing variabel bebas.
Interpretasi terhadap persamaan juga relatif sama, sebagai ilustrasi, pengaruh antara motivasi (X1), kompensasi (X2) dan kepemimpinan (X3) terhadap kepuasan kerja (Y) menghasilkan persamaan sebagai berikut:
Y = 0,235 + 0,21 X1 + 0,32 X2 + 0,12 X3
Jika variabel motivasi meningkat dengan asumsi variabel kompensasi dan kepemimpinan tetap, maka kepuasan kerja juga akan meningkat
Jika variabel kompensasi meningkat, dengan asumsi variabel motivasi dan kepemimpinan tetap, maka kepuasan kerja juga akan meningkat.
Jika variabel kepemimpinan meningkat, dengan asumsi variabel motivasi dan kompensasi tetap, maka kepuasan kerja juga akan meningkat.
Interpretasi terhadap konstanta (0,235) juga harus dilakukan secara hati-hati. Jika pengukuran variabel dengan menggunakan skala Likert antara 1 sampai dengan 5 maka tidak boleh diinterpretasikan bahwa jika variabel motivasi, kompensasi dan kepemimpinan bernilai nol, karena ketiga variabel tersebut tidak mungkin bernilai nol karena Skala Likert terendah yang digunakan adalah 1.
Analisis regresi linear berganda memerlukan pengujian secara serempak dengan menggunakan F hitung. Signifikansi ditentukan dengan membandingkan F hitung dengan F tabel atau melihat signifikansi pada output SPSS. Dalam beberapa kasus dapat terjadi bahwa secara simultan (serempak) beberapa variabel mempunyai pengaruh yang signifikan, tetapi secara parsial tidak. Sebagai ilustrasi: seorang penjahat takut terhadap polisi yang membawa pistol (diasumsikan polisis dan pistol secara serempak membuat takut penjahat). Akan tetapi secara parsial, pistol tidak membuat takut seorang penjahat. Contoh lain: air panas, kopi dan gula menimbulkan kenikmatan, tetapi secara parsial, kopi saja belum tentu menimbulkan kenikmatan.
Penggunaan metode analisis regresi linear berganda memerlukan uji asumsi klasik yang secara statistik harus dipenuhi. Asumsi klasik yang sering digunakan adalah asumsi normalitas, multikolinearitas, autokorelasi, heteroskedastisitas dan asumsi linearitas..
Bentuk-bentuk regresi yang juga sering digunakan dalam penelitian adalah regresi logistik atau regresi ordinal.
Pertanyaan-pertanyaan yang sering muncul
Dalam uji regresi sederhana apakah perlu menginterpretasikan nilai F hitung?
Uji F adalah uji kelayakan model (goodness of fit) yang harus dilakukan dalam analisis regresi linear. Untuk analisis regresi linear sederhana Signifikansi pada Uji F sama hasilnya dengan signifikansi pada uji t.
Kapan menggunakan uji satu arah dan kapan menggunakan uji dua arah?
Apa bedanya korelasi dengan regresi?
Gallery Analisis Regresi Linear Berganda
 Cara Melakukan Analisis Regresi Multiples Berganda Dengan
Cara Melakukan Analisis Regresi Multiples Berganda Dengan
 Pengertian Dan Contoh Kasus Uji Regresi Linear Sederhana Dan
Pengertian Dan Contoh Kasus Uji Regresi Linear Sederhana Dan
 Jam Statistic Contoh Analisis Regresi Linear Berganda Dua
Jam Statistic Contoh Analisis Regresi Linear Berganda Dua
Analisa Permodelan Bangkitan Pergerakan Lalu Lintas Pada
 Analisis Regresi Linier Berganda
Analisis Regresi Linier Berganda
 Analisis Regresi Linear Berganda Adalah Hubungan Secara
Analisis Regresi Linear Berganda Adalah Hubungan Secara
 Makalah Regresi Linear Berganda Docx Document
Makalah Regresi Linear Berganda Docx Document
 Analisis Regresi Linear Berganda Dengan Software R
Analisis Regresi Linear Berganda Dengan Software R

 Uji Analisis Regresi Linear Ganda Dengan Spss Konsistensi
Uji Analisis Regresi Linear Ganda Dengan Spss Konsistensi
 Ppt Regresi Linier Berganda Powerpoint Presentation Free
Ppt Regresi Linier Berganda Powerpoint Presentation Free
 Analisis Regresi Linear Berganda Dengan Spss Metode Enter Vs
Analisis Regresi Linear Berganda Dengan Spss Metode Enter Vs
 Penjelasan Dan Tutorial Regresi Linear Berganda Uji Statistik
Penjelasan Dan Tutorial Regresi Linear Berganda Uji Statistik
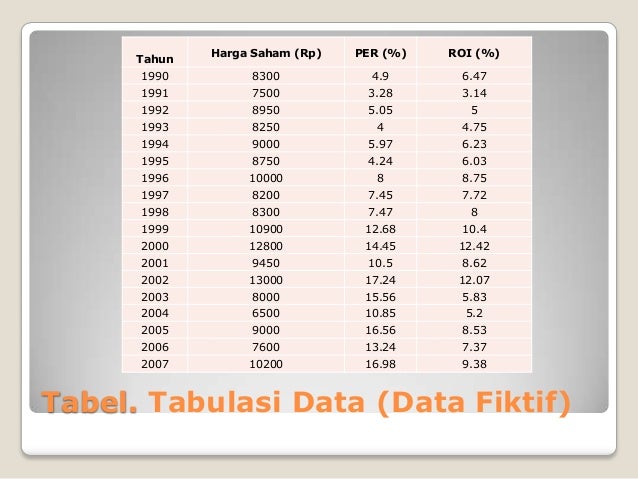 Analisis Regresi Linier Berganda
Analisis Regresi Linier Berganda
 Pengertian Dan Contoh Soal Regresi Linier Berganda Statmat Id
Pengertian Dan Contoh Soal Regresi Linier Berganda Statmat Id
 Uji Analisis Regresi Linear Ganda Dengan Spss Konsistensi
Uji Analisis Regresi Linear Ganda Dengan Spss Konsistensi
 Pengertian Dan Contoh Soal Regresi Linier Berganda Statmat Id
Pengertian Dan Contoh Soal Regresi Linier Berganda Statmat Id

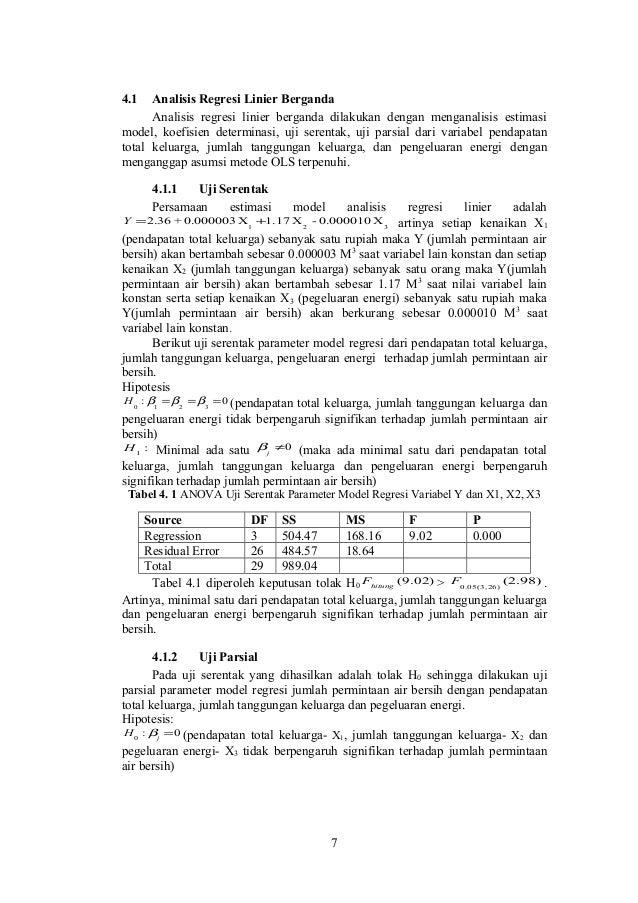 Analisis Regresi Linier Berganda Dan Pengujian Asumsi Residual
Analisis Regresi Linier Berganda Dan Pengujian Asumsi Residual
 Analisis Regresi Linear Berganda Dengan Spss Metode Enter Vs
Analisis Regresi Linear Berganda Dengan Spss Metode Enter Vs

 Contoh Regresi Linier Sederhana Dengan Spss Ariestha
Contoh Regresi Linier Sederhana Dengan Spss Ariestha
 Analisis Regresi Linier Berganda
Analisis Regresi Linier Berganda
 Analisis Regresi Linear Berganda Docx 2 1 1 Analisis
Analisis Regresi Linear Berganda Docx 2 1 1 Analisis
0 Response to "Analisis Regresi Linear Berganda"
Post a Comment