Uji Chi Square Spss
 Step By Step Chi Square Test With Crosstabs In Spss Complete
Step By Step Chi Square Test With Crosstabs In Spss Complete
STATISTIKA 2 (UJI CHI SQUARE)

BAB I
PENDAHULUAN
Chi-Square disebut juga dengan Kai Kuadrat. Chi Square adalah salah satu jenis uji komparatif non parametris yang dilakukan pada dua variabel, di mana skala data kedua variabel adalah nominal. (Apabila dari 2 variabel, ada 1 variabel dengan skala nominal maka dilakukan uji chi square dengan merujuk bahwa harus digunakan uji pada derajat yang terendah).
Uji chi-square merupakan uji non parametris yang paling banyak digunakan. Namun perlu diketahui syarat-syarat uji ini adalah: frekuensi responden atau sampel yang digunakan besar, sebab ada beberapa syarat di mana chi square dapat digunakan yaitu:
- Tidak ada cell dengan nilai frekuensi kenyataan atau disebut juga Actual Count (F0) sebesar 0 (Nol).
- Apabila bentuk tabel kontingensi 2 X 2, maka tidak boleh ada 1 cell saja yang memiliki frekuensi harapan atau disebut juga expected count (“Fh”) kurang dari 5.
- Apabila bentuk tabel lebih dari 2 x 2, misak 2 x 3, maka jumlah cell dengan frekuensi harapan yang kurang dari 5 tidak boleh lebih dari 20%.
- Apa yang dimaksud dengan uji chi square ?
- Bagaimana rumus chi square ?
- Bagaimana analisis uji chi square ?
- Bagaimana table chi square ?
- Bagaimana menguji independensi antara 2 faktor ?
- Bagaimana cara menguji proporsi ?
- Untuk mengetahui apa yang dimaksud dengan uji chi square
- Untuk mengetahui bagaimana rumus chi square
- Untuk mengetahui bagaimana analisis uji chi square
- Untuk mengetahui bagaimana table chi square
- Untuk mengetahui bagaimana menguji independensi antara 2 faktor
- Untuk mengetahui bagaimana cara menguji proporsi.
BAB II
PEMBAHASAN
Metode Uji Chi Square
Chi-Square disebut juga dengan Kai Kuadrat. Chi Square adalah salah satu jenis uji komparatif non parametris yang dilakukan pada dua variabel, di mana skala data kedua variabel adalah nominal. (Apabila dari 2 variabel, ada 1 variabel dengan skala nominal maka dilakukan uji chi square dengan merujuk bahwa harus digunakan uji pada derajat yang terendah).
Uji chi-square merupakan uji non parametris yang paling banyak digunakan. Namun perlu diketahui syarat-syarat uji ini adalah: frekuensi responden atau sampel yang digunakan besar, sebab ada beberapa syarat di mana chi square dapat digunakan yaitu:
- Tidak ada cell dengan nilai frekuensi kenyataan atau disebut juga Actual Count (F0) sebesar 0 (Nol).
- Apabila bentuk tabel kontingensi 2 X 2, maka tidak boleh ada 1 cell saja yang memiliki frekuensi harapan atau disebut juga expected count (“Fh”) kurang dari 5.
- Apabila bentuk tabel lebih dari 2 x 2, misak 2 x 3, maka jumlah cell dengan frekuensi harapan yang kurang dari 5 tidak boleh lebih dari 20%.
Rumus chi-square sebenarnya tidak hanya ada satu. Apabila tabel kontingensi bentuk 2 x 2, maka rumus yang digunakan adalah “koreksi yates”.
Apabila tabel kontingensi 2 x 2 seperti di atas, tetapi tidak memenuhi syarat seperti di atas, yaitu ada cell dengan frekuensi harapan kurang dari 5, maka rumus harus diganti dengan rumus “Fisher Exact Test”.
Pada artikel ini, akan fokus pada rumus untuk tabel kontingensi lebih dari 2 x 2, yaitu rumus yang digunakan adalah “Pearson Chi-Square”.
Rumus Tersebut adalah:
Uji kai kuadrat (dilambangkan dengan “χ2” dari huruf Yunani “Chi” dilafalkan “Kai”) digunakan untuk menguji dua kelompok data baik variabel independen maupun dependennya berbentuk kategorik atau dapat juga dikatakan sebagai uji proporsi untuk dua peristiwa atau lebih, sehingga datanya bersifat diskrit. Misalnya ingin mengetahui hubungan antara status gizi ibu (baik atau kurang) dengan kejadian BBLR (ya atau tidak).
Dasar uji kai kuadrat itu sendiri adalah membandingkan perbedaan frekuensi hasil observasi (O) dengan frekuensi yang diharapkan (E). Perbedaan tersebut meyakinkan jika harga dari Kai Kuadrat sama atau lebih besar dari suatu harga yang ditetapkan pada taraf signifikan tertentu (dari tabel χ2).
Uji Kai Kuadrat dapat digunakan untuk menguji :
- Uji χ2 untuk ada tidaknya hubungan antara dua variabel (Independency test).
- Uji χ2 untuk homogenitas antar- sub kelompok (Homogenity test).
- Uji χ2 untuk Bentuk Distribusi (Goodness of Fit)
Sebagai rumus dasar dari uji Kai Kuadrat adalah :
Keterangan :
O = frekuensi hasil observasi
E = frekuensi yang diharapkan.
Nilai E = (Jumlah sebaris x Jumlah Sekolom) / Jumlah data
df = (b-1) (k-1)
Dalam melakukan uji kai kuadrat, harus memenuhi syarat:
- Sampel dipilih secara acak
- Semua pengamatan dilakukan dengan independen
- Setiap sel paling sedikit berisi frekuensi harapan sebesar 1 (satu). Sel-sel dengdan frekuensi harapan kurang dari 5 tidak melebihi 20% dari total sel
- Besar sampel sebaiknya > 40 (Cochran, 1954)
Keterbatasan penggunaan uji Kai Kuadrat adalah tehnik uji kai kuadarat memakai data yang diskrit dengan pendekatan distribusi kontinu.Dekatnya pendekatan yang dihasilkan tergantung pada ukuran pada berbagai sel dari tabel kontingensi. Untuk menjamin pendekatan yang memadai digunakan aturan dasar “frekuensi harapan tidak boleh terlalu kecil” secara umum dengan ketentuan:
- Tidak boleh ada sel yang mempunyai nilai harapan lebih kecil dari 1 (satu)
- Tidak lebih dari 20% sel mempunyai nilai harapan lebih kecil dari 5 (lima)
Bila hal ini ditemukan dalam suatu tabel kontingensi, cara untuk menanggulanginyanya adalah dengan menggabungkan nilai dari sel yang kecil ke se lainnya (mengcollaps), artinya kategori dari variabel dikurangi sehingga kategori yang nilai harapannya kecil dapat digabung ke kategori lain. Khusus untuk tabel 2×2 hal ini tidak dapat dilakukan, maka solusinya adalah melakukan uji
“Fisher Exact atau Koreksi Yates” Analisis Chi Square Contoh kasus
Perusahaan penyalur alat elektronik AC ingin mengetahui apakah ada hubungan antara gender dengan sikap mereka terhadap kualitas produk AC. Untuk itu mereka meminta 25 responden mengisi identitas mereka dan sikap atau persepsi mereka terhadap produknya.
Permasalahan : Apakah ada hubungan antara gender dengan sikap terhadap kualitas AC?
Hipotesis :
- H0 = Tidak ada hubungan antara gender dengan sikap terhadap kualitas AC
- H1 = Ada hubungan antara gender dengan sikap terhadap kualitas AC
Tolak hipotesis nol (H0) apabila nilai signifikansi chi-square < 0.05 atau nilai chi-square hitung lebih besar (>) dari nilai chi-square tabel.
- Menguji Independensi antara 2 faktor (independensi)
Independensi (keterkaitan) antara 2 faktor dapat diuji dengan uji chi square. Masalah independensi ini banyak mendapat perhatian hampir di semua bidang, baik eksakta maupun sosial ekonomi. Kita ambil contoh di bidang ekonomi dan pendidikan. Kita bisa menduga bahwa keadaan ekonomi seseorang tidak ada kaitannya dengan tingkat pendidikannya, atau justru sebaliknya bahwa keadaan ekonomi seseorang terkait erat dengan tingkat pendidikannya. Untuk menjawab dugaan-dugaan ini, kita bisa menggunakan uji chi square. Langkah-langkahnya sebagai berikut.
- Buatlah hipotesis H0: tidak ada kaitan antara keadaan ekonomi seseorang dengan pendidikannya
HA: ada kaitan antara keadaan ekonomi seseorang dengan pendidikannya
- Lakukan penelitian dan kumpulkan data
Hasil penelitian adalah sebagai berikut (tentatif).
| Kategori | Di bawah garis kemiskinan | Di atas garis kemiskinan | Total |
| Tidak tamat SD | 8 | 4 | 12 |
| SD | 20 | 17 | 37 |
| SMP | 15 | 16 | 31 |
| SMA | 3 | 23 | 26 |
| Perguruan Tinggi | 2 | 22 | 24 |
| Total | 48 | 82 | 130 |
| Kategori | Di bawah garis kemiskinan | Di atas garis kemiskinan | Total |
| Tidak tamat SD O E | 8 4,43 | 4 7,57 | 12 |
| SD O E | 20 13,66 | 17 23,34 | 37 |
| SMP O E | 15 11,45 | 16 19,55 | 31 |
| SMA O E | 3 9,60 | 23 16,40 | 26 |
| Perguruan Tinggi O E | 2 8,86 | 22 15,14 | 24 |
| Total | 48 | 82 | 130 |
Nilai O (Observasi) adalah nilai pengamatan di lapangan Nilai E (expected) adalah nilai yang diharapkan, dihitung sbb: 1. Nilai E untuk kategori tidak tamat SD di bawah garis kemiskinan= (12 x 48)/130 = 4,43 2. Nilai E untuk kategori tidak tamat SD di atas garis kemiskinan = (12 x 82)/130 = 7,57 3. Nilai E untuk kategori SD di bawah garis kemiskinan = (37 x 48)/130 = 13,66 4. Nilai E untuk kategori SD di atas garis kemiskinan = (37 x 82)/130 = 23,34 5. Nilai E untuk kategori SMP di bawah garis kemiskinan = (31 x 48)/130 = 11,45 6. Nilai E untuk kategori SMP di atas garis kemiskinan = (31 x 82)/130 = 19,55 7. Nilai E untuk kategori SMA di bawah garis kemiskinan = (26 x 48)/130 = 9,60 8. Nilai E untuk kategori SMA di atas garis kemiskinan = (26 x 82)/130 = 16,40 9. Nilai E untuk kategori Perguruan Tinggi di bawah garis kemiskinan = (24 x 48)/130 = 8,86
10. Nilai E untuk kategori Perguruan Tinggi di atas garis kemiskinan = (24 x 82)/130 = 15,14
Gallery Uji Chi Square Spss
Tutorial Mudah Mahir Uji Chi Square Tabel 2xk Spss
 Uji Chi Square Dengan Spss Parameter D
Uji Chi Square Dengan Spss Parameter D
 Step By Step Chi Square Test With Crosstabs In Spss Complete
Step By Step Chi Square Test With Crosstabs In Spss Complete
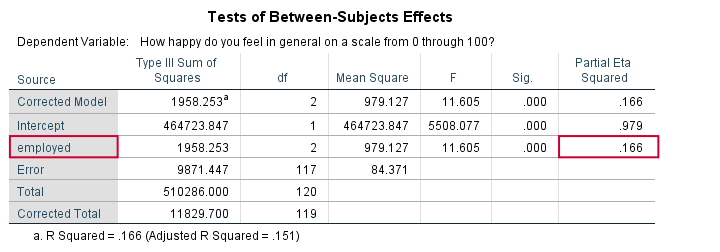 How To Get Partial Eta Squared From Spss
How To Get Partial Eta Squared From Spss
 Step By Step Chi Square Test With Crosstabs In Spss Complete
Step By Step Chi Square Test With Crosstabs In Spss Complete
Identifying Multivariate Outliers In Spss Statistics Solutions
 Uji Chi Square Dengan Spss Serta Interpretasi Lengkap Spss
Uji Chi Square Dengan Spss Serta Interpretasi Lengkap Spss
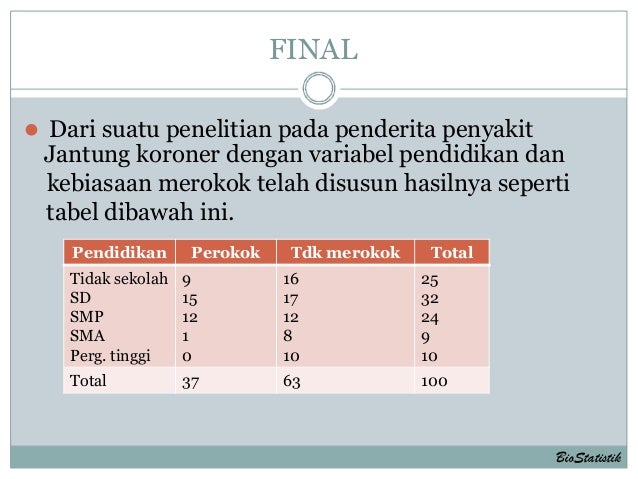 Uji Chi Square Secara Manual Dan Spss
Uji Chi Square Secara Manual Dan Spss
 Tutorial Statistik Analisis Chi Square
Tutorial Statistik Analisis Chi Square
 How To Use Spss Chi Square Test For Goodness Of Fit
How To Use Spss Chi Square Test For Goodness Of Fit
 Uji Chi Square Dengan Spss Serta Interpretasi Lengkap Spss
Uji Chi Square Dengan Spss Serta Interpretasi Lengkap Spss
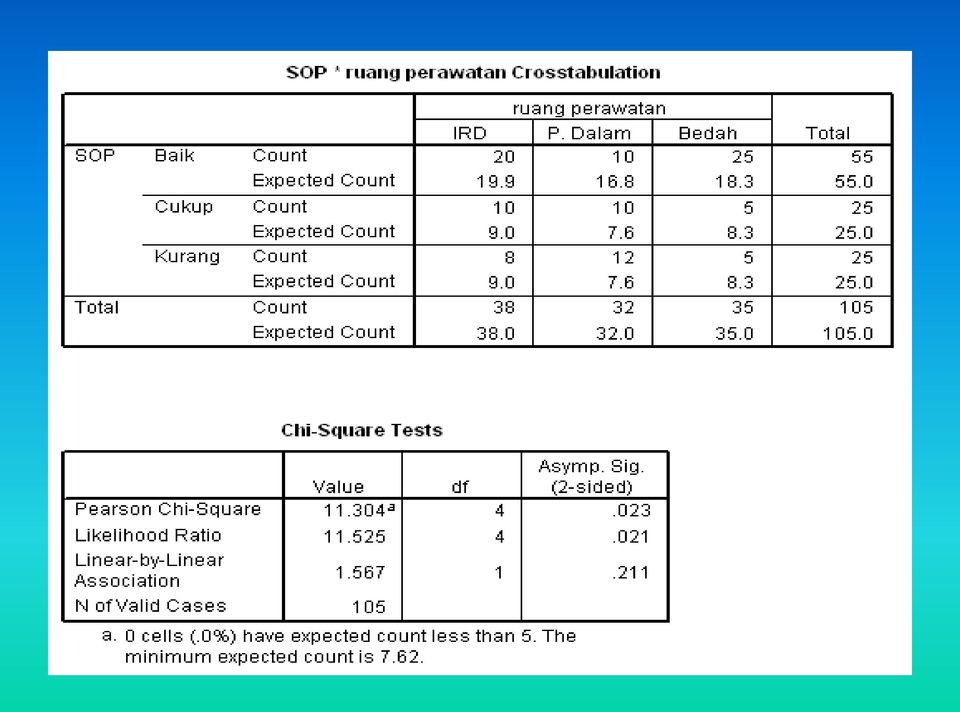 Uji Chi Square 2 Prinsip 1 Merupakan Analisis Data
Uji Chi Square 2 Prinsip 1 Merupakan Analisis Data
 Uji Chi Square Dengan Spss Serta Interpretasi Lengkap Spss
Uji Chi Square Dengan Spss Serta Interpretasi Lengkap Spss

 Using Chi Square To Perform Chi Square Tests1
Using Chi Square To Perform Chi Square Tests1
 Uji Chi Square Dan Fishers Exact Dengan Spss Dan Statcal
Uji Chi Square Dan Fishers Exact Dengan Spss Dan Statcal
 Uji Chi Square Dengan Spss Serta Interpretasi Lengkap Spss
Uji Chi Square Dengan Spss Serta Interpretasi Lengkap Spss
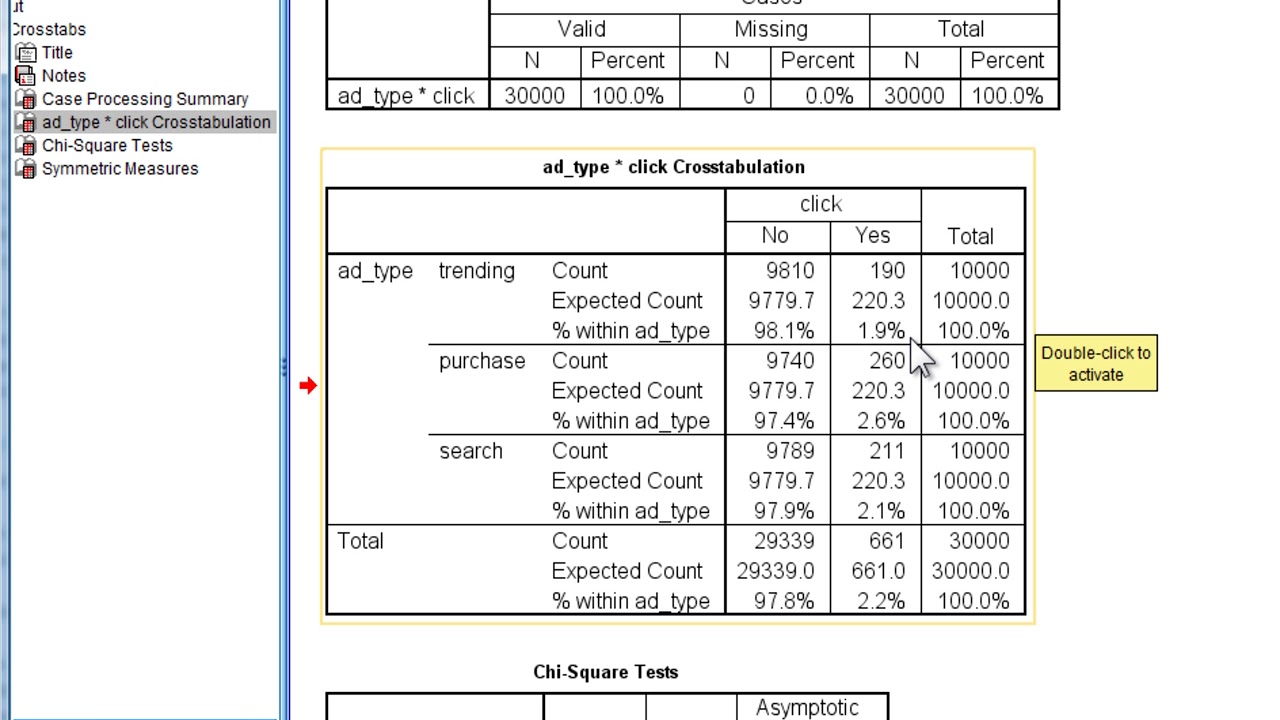 V4 10 R X C 2x3 Pearson Chi Square In Spss
V4 10 R X C 2x3 Pearson Chi Square In Spss
 Tutorial Cara Uji Chi Square Dengan Program Spss
Tutorial Cara Uji Chi Square Dengan Program Spss

 Alternatives Of Fisher S Exact Test For More Than 2 Groups
Alternatives Of Fisher S Exact Test For More Than 2 Groups
 Tutorial Rumus Chi Square Dan Metode Hitung Uji Statistik
Tutorial Rumus Chi Square Dan Metode Hitung Uji Statistik
 Uji Chi Square Dengan Spss Serta Interpretasi Lengkap Spss
Uji Chi Square Dengan Spss Serta Interpretasi Lengkap Spss
 Uji Chi Square Dengan Spss Parameter D
Uji Chi Square Dengan Spss Parameter D
 Step By Step Chi Square Test With Crosstabs In Spss Complete
Step By Step Chi Square Test With Crosstabs In Spss Complete
 Pdf Uji Chi Square Spss Fni Statistik Malang Fni
Pdf Uji Chi Square Spss Fni Statistik Malang Fni



0 Response to "Uji Chi Square Spss"
Post a Comment