Blog Koma - Pada artikel ini kita akan membahas materi
Limit Tak Hingga Fungsi Trigonometri. Materi
Limit Tak Hingga Fungsi Trigonometri merupakan gabungan bentuk
limit tak hingga dan
limit fungsi trigonometri. Jika kita perdalam lagi, ternyata bentuk "Limit Tak Hingga Fungsi Trigonometri" lebih menekankan pada limit fungsi trigonometrinya, sehingga teman-teman harus benar-benar menguasai materi limit fungsi trigonometrinya terlebih dahulu.
Bentuk tak hingga ($\infty$) jika sebagai sudut suatu fungsi trigonometri maka tidak bisa kita tentukan nilainya, misalkan $ \sin \infty, \cos \infty, \tan \infty $ tidak bisa kita tentukan nilainya karena nilai $ \sin x $ berkisar $ -1 \leq \sin x \leq 1 $, begitu juga nilai $ \cos x $ berkisar $ -1 \leq \cos x \leq 1 $ , dan untuk $ \tan x $ berkisar $ -\infty \leq \tan x \leq \infty $, tentu dengan $ x $ yang sudah pasti. Nah untuk memudahkan, maka bentuk yang diguankan adalah $ \frac{1}{\infty} = 0 $ sehingga nilai fungsi trigonometrinya bisa kita hitung yaitu $ \sin \frac{1}{\infty} = 0 , \cos \frac{1}{\infty} = 1, \tan \frac{1}{\infty} = 0 $ . Dan bentuk ini cocok dengan limit fungsi trigonometri yang akan kita bahas dalam artikel Limit Tak Hingga Fungsi Trigonometri.
![]()
Limit Tak Hingga Fungsi Trigonometri ini ternyata soalnya dikeluarkan pada SBMPTN 2017 matematika IPA atau matematika saintek satu soal disetiap kodenya. Nah, berlatar belakang dari inilah saya membahas artikel ini secara lebih khusus agar bisa membantu teman-teman yang ingin mempelajarinya atau siapa tahu tahun-tahun berikutnya akan keluar lagi di soal seleksi masuk PTN lainnya. Dalam pembahasan Limit Tak Hingga Fungsi Trigonometri, kita harus menguasai sifat-sifat limit fungsi trigonometri, rumus-rumus dasar trigonometri, dan limit tak hingga bentuk aljabar.
Sifat-sifat limit fungsi Trigonometri
$\clubsuit $ Sifat-sifat limit fungsi trigonometri i). $ \displaystyle \lim_{x \to 0 } \frac{\sin ax }{bx} = \frac{a}{b} \, \, $ atau $ \, \, \displaystyle \lim_{x \to 0 } \frac{ ax }{\sin bx} = \frac{a}{b} $ ii). $ \displaystyle \lim_{x \to 0 } \frac{\tan ax }{bx} = \frac{a}{b} \, \, $ atau $ \, \, \displaystyle \lim_{x \to 0 } \frac{ ax }{\tan bx} = \frac{a}{b} $ iii). $ \displaystyle \lim_{x \to 0 } \frac{\sin ax }{\sin bx} = \frac{a}{b} \, \, $ atau $ \, \, \displaystyle \lim_{x \to 0 } \frac{ \tan ax }{\tan bx} = \frac{a}{b} $
iv). $ \displaystyle \lim_{x \to 0 } \frac{\sin ax }{\tan bx} = \frac{a}{b} \, \, $ atau $ \, \, \displaystyle \lim_{x \to 0 } \frac{ \tan ax }{\sin bx} = \frac{a}{b} $
Rumus-rumus dasar Trigonometri
$\spadesuit $ Beberapa rumus yang digunakan dalam limit fungsi trigonometri : i). $ 1 - \cos px = 2\sin \frac{1}{2} px . \sin \frac{1}{2} px $ ii). $ \cos A - \cos B = -2\sin \frac{1}{2}(A+B) .\sin \frac{1}{2}(A-B) $ iii). Identitas trigonometri :
$ \sin ^2 x + \cos ^2 x = 1 \rightarrow 1 - \cos ^2 x = \sin ^2 x $
Limit tak hingga fungsi aljabar
$\clubsuit $ Limit tak hingga pecahan : Misalkan fungsinya $ f(x) = ax^n + a_1x^{n-1} + ... \, $ dengan pangkat tertinggi $ n \, $ dan $ g(x) = bx^m + b_1 x^{m-1} + .... $ dengan pangkat tertinggi $ m \, $ , maka limit di tak hingganya : $ \displaystyle \lim_{x \to \infty } \frac{ax^n + a_1x^{n-1} + ...}{bx^m + b_1 x^{m-1} + ....} \left\{ \begin{array}{ccc} = \frac{0}{b} & = 0 & , \text{untuk } n < m \\ = \frac{a}{b} & & , \text{untuk } n = m \\ = \frac{a}{0} & = \infty & , \text{untuk } n > m \end{array} \right. $
Catatan : Ambil koefisien pangkat tertingginya.
Contoh Soal Limit Tak Hingga Fungsi Trigonometri : 1). Tentukan hasil limit berikut ini : a). $ \displaystyle \lim_{x \to \infty } \, x \tan \frac{1}{x} $ b). $ \displaystyle \lim_{y \to \infty } \, \frac{1}{y} \cot \frac{1}{y} $ c). $ \displaystyle \lim_{x \to \infty } \, \frac{ \csc \frac{1}{x} }{x} $ Penyelesaian : a). Misalkan $ \frac{1}{x} = y $ , sehingga $ x = \frac{1}{y} $ . Untuk $ x $ mendekati $ \infty $ maka $ y $ mendekati $ 0 $. *). Menyelesaikan limitnya : $ \begin{align} \displaystyle \lim_{x \to \infty } \, x \tan \frac{1}{x} & = \displaystyle \lim_{y \to 0 } \, \frac{1}{y} \tan y \\ & = \displaystyle \lim_{y \to 0 } \, \frac{ \tan y }{y} \\ & = 1 \end{align} $ b). Misalkan $ \frac{1}{y} = x $ , dan $ \cot x = \frac{1}{\tan x} $ . Untuk $ y $ mendekati $ \infty $ maka $ x $ mendekati $ 0 $. *). Menyelesaikan limitnya : $ \begin{align} \displaystyle \lim_{y \to \infty } \, \frac{1}{y} \cot \frac{1}{y} & = \displaystyle \lim_{x \to 0 } \, x \cot x \\ & = \displaystyle \lim_{x \to 0 } \, x . \frac{1}{\tan x} \\ & = \displaystyle \lim_{x \to 0 } \, \frac{x}{\tan x} \\ & = 1 \end{align} $ c). Misalkan $ \frac{1}{x} = y $ , dan $ \csc y = \frac{1}{\sin y} $ . Untuk $ x $ mendekati $ \infty $ maka $ y $ mendekati $ 0 $. *). Menyelesaikan limitnya : $ \begin{align} \displaystyle \lim_{x \to \infty } \, \frac{ \csc \frac{1}{x} }{x} & = \displaystyle \lim_{x \to \infty } \, \frac{1}{x} . \csc \frac{1}{x} \\ & = \displaystyle \lim_{y \to 0 } \, y . \csc y \\ & = \displaystyle \lim_{y \to 0 } \, y . \frac{1}{\sin y} \\ & = \displaystyle \lim_{y \to 0 } \, \frac{y}{\sin y} \\ & = 1 \end{align} $ 2). Tentukan hasil limit tak kingga fungsi trigonometri berikut ini : a). $ \displaystyle \lim_{x \to \infty } \, \tan \frac{5}{x} . \csc \frac{2}{x} $ b). $ \displaystyle \lim_{x \to \infty } \, \cot 3x^{-1} . \sin x^{-1} $ b). $ \displaystyle \lim_{x \to \infty } \, \frac{\cot \frac{1}{2x}}{\csc \frac{3}{x}} $ Penyelesaian : a). Misalkan $ \frac{1}{x} = y $ , dan $ \csc y = \frac{1}{\sin y} $ . Untuk $ x $ mendekati $ \infty $ maka $ y $ mendekati $ 0 $. *). Menyelesaikan limitnya : $ \begin{align} \displaystyle \lim_{x \to \infty } \, \tan \frac{5}{x} . \csc \frac{2}{x} & = \displaystyle \lim_{y \to 0 } \, \tan 5y . \csc 2y \\ & = \displaystyle \lim_{y \to 0 } \, \tan 5y . \frac{1}{\sin 2y} \\ & = \displaystyle \lim_{y \to 0 } \, \frac{\tan 5y}{\sin 2y} \\ & = \frac{5}{2} \end{align} $ b). Misalkan $ \frac{1}{x} = y $ , dan $ \cot y = \frac{1}{\tan y} $ . Untuk $ x $ mendekati $ \infty $ maka $ y $ mendekati $ 0 $. *). Menyelesaikan limitnya : $ \begin{align} \displaystyle \lim_{x \to \infty } \, \cot 3x^{-1} . \sin x^{-1} & = \displaystyle \lim_{x \to \infty } \, \cot \frac{3}{x} . \sin \frac{1}{x} \\ & = \displaystyle \lim_{y \to 0 } \, \cot 3y . \sin y \\ & = \displaystyle \lim_{y \to 0 } \, \frac{1}{\tan 3y} . \sin y \\ & = \displaystyle \lim_{y \to 0 } \, \frac{\sin y}{\tan 3y} \\ & = \frac{1}{3} \end{align} $ c). Misalkan $ \frac{1}{x} = y $ , dan $ \csc y = \frac{1}{\sin y} $ . Untuk $ x $ mendekati $ \infty $ maka $ y $ mendekati $ 0 $. *). Menyelesaikan limitnya : $ \begin{align} \displaystyle \lim_{x \to \infty } \, \frac{\cot \frac{1}{2x}}{\csc \frac{3}{x}} & = \displaystyle \lim_{y \to 0 } \, \frac{\cot \frac{1}{2}y}{\csc 3y} \\ & = \displaystyle \lim_{y \to 0 } \, \frac{\frac{1}{\tan \frac{1}{2}y}}{\frac{1}{\sin 3y}} \\ & = \displaystyle \lim_{y \to 0 } \, \frac{\sin 3y}{\tan \frac{1}{2}y} \\ & = \frac{3}{ \frac{1}{2} } = 6 \end{align} $ 3). Tentukan hasil limit tak kingga fungsi trigonometri $ \displaystyle \lim_{y \to \infty } \, \sqrt{6y}\cos \frac{3}{\sqrt{y}} \sin \frac{5}{\sqrt{y}} $? Penyelesaian : *). Misalkan $ \frac{1}{\sqrt{y}} = x $ , sehingga $ \sqrt{y} = \frac{1}{x} $ . Untuk $ y $ mendekati $ \infty $ maka $ x $ mendekati $ 0 $. *). Menyelesaikan limitnya : $ \begin{align} \displaystyle \lim_{y \to \infty } \, \sqrt{6y}\cos \frac{3}{\sqrt{y}} \sin \frac{5}{\sqrt{y}} & = \displaystyle \lim_{y \to \infty } \, \sqrt{6}.\sqrt{y}\cos \frac{3}{\sqrt{y}} \sin \frac{5}{\sqrt{y}} \\ & = \displaystyle \lim_{x \to 0 } \, \sqrt{6}.\frac{1}{x} \cos 3x \sin 5x \\ & = \displaystyle \lim_{x \to 0 } \, \sqrt{6}. \cos 3x . \frac{\sin 5x}{x} \\ & = \displaystyle \lim_{x \to 0 } \, \sqrt{6} \cos 3x . \displaystyle \lim_{x \to 0 } \frac{\sin 5x}{x} \\ & = \sqrt{6} . \cos 0 . 5 \\ & = \sqrt{6}. 1 . 5 = 5\sqrt{6} \end{align} $ 4). $ \displaystyle \lim_{x \to \infty } \, \frac{1 - \cos \frac{4}{x}}{ \frac{1}{x} . \tan \frac{3}{x}} = .... ? $ Penyelesaian : *). Misalkan $ \frac{1}{x} = y $. Untuk $ x $ mendekati $ \infty $ maka $ y $ mendekati $ 0 $. Bentuk $ 1 - \cos 4y = 2\sin 2y. \sin 2y $ *). Menyelesaikan limitnya : $ \begin{align} \displaystyle \lim_{x \to \infty } \, \frac{1 - \cos \frac{4}{x}}{ \frac{1}{x} . \tan \frac{3}{x}} & = \displaystyle \lim_{y \to 0 } \, \frac{1 - \cos 4y}{ y . \tan 3y} \\ & = \displaystyle \lim_{y \to 0 } \, \frac{2\sin 2y. \sin 2y}{ y . \tan 3y} \\ & = \displaystyle \lim_{y \to 0 } \, \frac{2\sin 2y}{ y } . \displaystyle \lim_{y \to 0 } \, \frac{ \sin 2y}{\tan 3y} \\ & = 2.2 .\frac{2}{3} = \frac{8}{3} \end{align} $ 5). Tentukan hasil limit $ \displaystyle \lim_{x \to \infty } \, \frac{2x \cot \frac{2}{x} - 3 \cot \frac{2}{x}}{5x^2 - 2x} $ Penyelesaian : *). Misalkan $ \frac{1}{x} = y $ dan $ \cot y = \frac{1}{\tan y} $ Untuk $ x $ mendekati $ \infty $ maka $ y $ mendekati $ 0 $. *). Menyelesaikan limitnya : $ \begin{align} \displaystyle \lim_{x \to \infty } \, \frac{2x \cot \frac{2}{x} - 3 \cot \frac{2}{x}}{5x^2 - 2x} & = \displaystyle \lim_{x \to \infty } \, \frac{(2x - 3) \cot \frac{2}{x}}{x(5x - 2)} \\ & = \displaystyle \lim_{x \to \infty } \, \frac{(2x - 3) }{5x - 2} . \frac{1}{x} . \cot \frac{2}{x} \\ & = \displaystyle \lim_{x \to \infty } \, \frac{(2x - 3) }{5x - 2} . \displaystyle \lim_{x \to \infty } \, \frac{1}{x} . \cot \frac{2}{x} \\ & = \frac{2}{5}. \displaystyle \lim_{y \to 0 } \, y . \cot 2y \\ & = \frac{2}{5}. \displaystyle \lim_{y \to 0 } \, y . \frac{1}{\tan 2y} \\ & = \frac{2}{5}. \displaystyle \lim_{y \to 0 } \, \frac{y}{\tan 2y} \\ & = \frac{2}{5}. \frac{1}{2} = \frac{1}{5} \end{align} $ 6). $ \displaystyle \lim_{x \to \infty } \frac{\cos \frac{4}{x}+ \cos \frac{2}{x}.\sin \frac{3}{\sqrt{x}} - \cos \frac{4}{x}.\sin \frac{3}{\sqrt{x}} - \cos \frac{2}{x}}{\sin ^2 \frac{1}{x} - \cos \frac{2}{x} + 1}= ...?$ Penyelesaian : *). Misalkan $ \frac{1}{x} = y $, maka $ \frac{1}{\sqrt{x}} = \sqrt{y} $ Untuk $ x $ mendekati $ \infty $ maka $ y $ mendekati $ 0 $. *). Mengubah bentuk soalnya : $ \begin{align} & \displaystyle \lim_{x \to \infty } \frac{\cos \frac{4}{x}+ \cos \frac{2}{x}.\sin \frac{3}{\sqrt{x}} - \cos \frac{4}{x}.\sin \frac{3}{\sqrt{x}} - \cos \frac{2}{x}}{\sin ^2 \frac{1}{x} - \cos \frac{2}{x} + 1} \\ & = \displaystyle \lim_{y \to 0 } \frac{\cos 4y+ \cos 2y.\sin 3\sqrt{y} - \cos 4y.\sin 3\sqrt{y} - \cos2y}{\sin ^2 y - \cos 2y + 1} \end{align} $ *). Mengubah bentuk pembilang dan penyebutnya : -). Pembilangnya, Rumus $ \cos A - \cos B = -2 \sin \frac{1}{2}(A+B).\sin \frac{1}{2}(A-B) $ $ \begin{align} & \cos 4y+ \cos 2y.\sin 3\sqrt{y} - \cos 4y.\sin 3\sqrt{y} - \cos2y \\ & = \cos 4y - \cos 4y. \sin 3\sqrt{y} - \cos 2y + \cos 2y . \sin 3\sqrt{y} \\ & = \cos 4y ( 1 - \sin 3\sqrt{y} ) - \cos 2y ( 1 - \sin 3\sqrt{y} ) \\ & = (\cos 4y - \cos 2y) ( 1 - \sin 3\sqrt{y} ) \\ & = (-2 \sin \frac{1}{2}(4y+2y). \sin \frac{1}{2}(4y-2y)) ( 1 - \sin 3\sqrt{y} ) \\ & = -2 \sin 3y. \sin y. ( 1 - \sin 3\sqrt{y} ) \end{align} $ -). Penyebutnya, Rumus $ 1 - \cos px = 2 \sin \frac{1}{2} px . \sin \frac{1}{2} px $ $ \begin{align} \sin ^2 y - \cos 2y + 1 & = \sin ^2 y + (1 - \cos 2y) \\ & = \sin ^2 y + 2\sin y . \sin y \\ & = 3\sin y . \sin y \end{align} $ *). Menyelesaikan limitnya : $ \begin{align} & \displaystyle \lim_{y \to 0 } \frac{\cos 4y+ \cos 2y.\sin 3\sqrt{y} - \cos 4y.\sin 3\sqrt{y} - \cos2y}{\sin ^2 y - \cos 2y + 1} \\ & = \displaystyle \lim_{y \to 0 } \frac{-2 \sin 3y. \sin y. ( 1 - \sin 3\sqrt{y} ) }{3\sin y . \sin y} \\ & = \displaystyle \lim_{y \to 0 } \frac{-2 \sin 3y. ( 1 - \sin 3\sqrt{y} ) }{3\sin y } \\ & = \displaystyle \lim_{y \to 0 } \frac{\sin 3y}{\sin y} . \frac{-2}{3}( 1 - \sin 3\sqrt{y} ) \\ & = \displaystyle \lim_{y \to 0 } \frac{\sin 3y}{\sin y} . \displaystyle \lim_{y \to 0 } \frac{-2}{3}( 1 - \sin 3\sqrt{y} ) \\ & = 3 . \frac{-2}{3}( 1 - \sin 0 ) \\ & = 3 . \frac{-2}{3}( 1 - 0 ) \\ & = 3 . \frac{-2}{3}.( 1 ) = -2 \end{align} $
Berikut kami sajikan 4 soal limit tak hingga fungsi trigonometri yang keluar pada soal SBMPTN 2017 matematika IPA dari 4 kode berbeda:
Nomor 11 , Soal SBMPTN 2017 Kode 165 $ \displaystyle \lim_{y \to \infty } y . \sin \frac{3}{y}. \cos \frac{5}{y} = .... $ A). $ 0 \, $ B). $ 1 \, $ C). $ 2 \, $ D). $ 3 \, $ E). $ 4 $
Nomor 11, Soal SBMPTN 2017 Kode 166 $ \displaystyle \lim_{x \to \infty } \frac{\sin \frac{3}{x}}{\left(1 - \cos \frac{2}{x} \right).x^2.\sin \frac{1}{x}} = .... $ A). $ 0 \, $ B). $ \frac{2}{3} \, $ C). $ 1 \, $ D). $ \frac{3}{2} \, $ E). $ 3 $
Nomor 11, Soal SBMPTN 2017 Kode 167 $ \displaystyle \lim_{x \to \infty } \, x\left(1 - \cos \frac{1}{\sqrt{x}} \right) = .... $ A). $ 1 \, $ B). $ \frac{1}{2} \, $ C). $ \frac{1}{3} \, $ D). $ \frac{1}{4} \, $ E). $ \frac{1}{5} $
Nomor 11, Soal SBMPTN 2017 Kode 168 $ \displaystyle \lim_{x \to \infty } \, 2x \tan \frac{1}{x}. \sec \frac{2}{x} = .... $ A). $ 0 \, $ B). $ 1 \, $ C). $ 2 \, $ D). $ 3 \, $ E). $ 4 $
Demikian pembahasan materi
Limit Tak Hingga Fungsi Trigonometri dan contohnya. Silahkan baca juga materi
Limit lainnya.
Artikel Terkait
 Limit Fungsi Semester 2 Kelas Xi Ipa 6 Ppt Download
Limit Fungsi Semester 2 Kelas Xi Ipa 6 Ppt Download 
 Limit Tak Hingga Fungsi Trigonometri 8 Youtube
Limit Tak Hingga Fungsi Trigonometri 8 Youtube Mathematic Center Limit Fungsi Trigonometri Tak Hingga


 Contoh Soal Limit Trigonometri Tak Hingga Pdf
Contoh Soal Limit Trigonometri Tak Hingga Pdf  Limit Fungsi Matematika Trigonometri Tak Hingga Contoh
Limit Fungsi Matematika Trigonometri Tak Hingga Contoh  Soal Limit Tak Hingga Dari Fungsi Yang Memuat Eksponen
Soal Limit Tak Hingga Dari Fungsi Yang Memuat Eksponen  Limit Fungsi Trigonometri Di Tak Hingga Brainly Co Id
Limit Fungsi Trigonometri Di Tak Hingga Brainly Co Id  Limit Tak Hingga F Trigonometri Soal Dan Pembahasan Youtube
Limit Tak Hingga F Trigonometri Soal Dan Pembahasan Youtube  Pembahasan Sbmptn 2017 Limit Tak Hingga Trigonometri
Pembahasan Sbmptn 2017 Limit Tak Hingga Trigonometri  Contoh Soal Limit Fungsi Trigonometri Menuju Tak Hingga
Contoh Soal Limit Fungsi Trigonometri Menuju Tak Hingga 
 Limit Tak Hingga Trigonometri Polinomial Pecahan Eksonensial
Limit Tak Hingga Trigonometri Polinomial Pecahan Eksonensial  Cara Cepat Menghitung Limit Fungsi Trigonometri Halaman All
Cara Cepat Menghitung Limit Fungsi Trigonometri Halaman All  Limit Fungsi Aljabar Tak Terhingga
Limit Fungsi Aljabar Tak Terhingga  Rumus Cepat Dalam Mengerjakan Limit Tak Hingga
Rumus Cepat Dalam Mengerjakan Limit Tak Hingga  Soal Limit Tak Hingga Fungsi Trigonometri 1
Soal Limit Tak Hingga Fungsi Trigonometri 1  10 Soal Dan Pembahasan Limit Fungsi Trigonometri
10 Soal Dan Pembahasan Limit Fungsi Trigonometri 

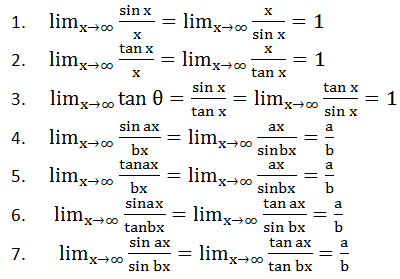 Contoh Soal Limit Tak Hingga Bentuk Trigonometri Tasticfasr
Contoh Soal Limit Tak Hingga Bentuk Trigonometri Tasticfasr 


0 Response to "Limit Tak Hingga Trigonometri"
Post a Comment