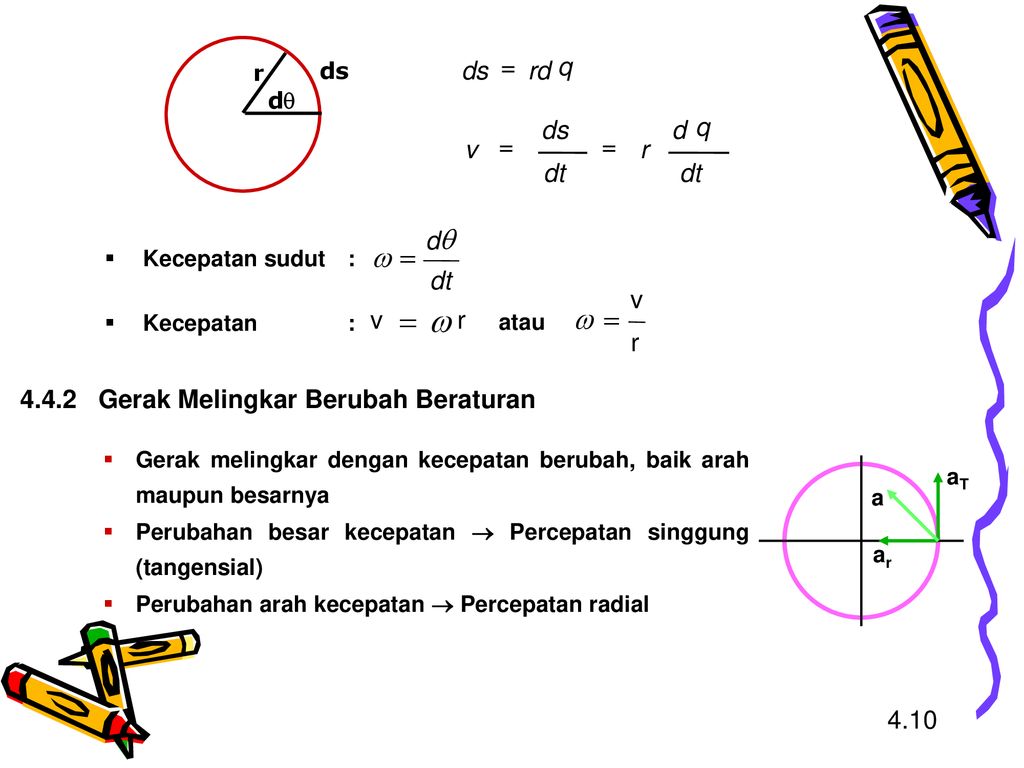
Gerak Melingkar Berubah Beraturan

Ppt Besaran Besaran Gerak Melingkar Powerpoint

Gerak Melingkar Beraturan dan Berubah Beraturan

Gerak Melingkar – Masih dalam pelajaran fisika, pelajaran kali ini kita akan membahasa mengenai gerak melingkar beraturan, berubah beraturan, rumus dan contoh soal beserta pengertian lengkapnya. Namun dipertemuan sebelumnya bersama kami telah membahas mengenai glbb. Baiklah langsung saja mari kita simak bersama penjelasannya di bawah ini.

Pengertian Gerak Melingkar

Gerak Melingkar ialah merupakan suatu gerakan atau objek yang lintasannya berupa lingkaran mengelilingi suatu titik tetap. Misalnya seperti halnya pada gerakan Bulan mengelilingi bumi dan gerakan berputar bola yang tergantung pada tali.

Gerak Melingkar Beraturan

(GMB) atau Gerak melingkar beraturan ialah merupakan gerak suatu benda yang menempuh lintasan melingkar dengan besar kecepatan tetap. Pada kecepatan GMB ini besarnya selalu statis/tetap, akan tetapi arahnya selalu berubah, dan arah kecepatan selalu menyinggung lingkaran. Jadi dapat diambil kesimpulan, arah kecepatan (v) selalu tegak lurus dengan garis yang ditarik melalui pusat lingkaran pada titik tangkap vektor kecepatan pada saat itu juga.

Besaran-Besaran Fisika dalam Gerak Melingkar

Periode (T) dan Frekuensi (f)

Waktu yang dibutuhkan suatu benda yang begerak melingkar untuk melakukan satu putaran penuh disebut periode. Pada umumnya periode diberi notasi T. Satuan SI periode adalah sekon (s).

Banyaknya jumlah putaran yang ditempuh oleh suatu benda yang bergerak melingkar dalam selang waktu satu sekon disebut frekuensi. Adapun artian dari SI sendiri ialah suatu putaran per sekon atau hertz (Hz). yang mempunyai hubungan antara periode dan frekuensi sebagai berikut.

Adapun Keteranganya : = yaitu banyak putaran = waktu (s) yang dibutuhkan 1putaran = rad(radian) 1rpm(rotasi per menit)= .

Keterangan:

T : periode (s)

f : frekuensi (Hz)

Kecepatan Linear

Apabila ada suatu benda yang dapat melakukan sebuah gerakan melingkar secara beraturan dengan arah gerak berlawanan arah jarum jam dan berawal dari titik A. Dengan memerlukan waktu guna untuk menempuh satu putaran yakni T. Yang dalam sekali putaran, benda tersebut sudah hampir mencapai lintasan linear sepanjang sekeliling ruas lingkaran (2 π r ), sedangkan r merupakan jarak benda dengan pusat lingkaran (O) atau jari-jari lingkaran. Kemudian pada kecepatan (v) ialah hasil pembagian dari panjang lintasan linear yang ditempuh benda dengan selang waktu tempuhnya.

Secara matematis dapat ditulis sebagai berikut.

Diketahui bahwa T = 1/f atau f = 1/T, jadi persamaan kecepatan linear dapat ditulis sebagai berikut:

Kecepatan Sudut (Kecepatan Anguler)

Sebelum mempelajari kecepatan sudut Anda pahami dulu tentang gerak jatuh bebas. SI ialah termasuk dalam suatu satuan perpindahan sudut bidang datar pada radian (rad). dan mempunyai nilai yakni suatu perbandingan antara jarak linear yang ditempuh benda dengan jari-jari lingkaran. Oleh karena satuan sudut yang biasa digunakan ialah derajat, maka perlu kita konversikan satuan sudut radian dengan derajat. Apabila diketahui bahwa keliling lingkaran ialah 2 π r. kemudian contohnya pada sudut pusat satu lingkarannya θ, jadi sudut pusat disebut 1 rad apabila pada sebuah busur yang ditempuh sama dengan jari-jarinya. Persamaan matematisnya ialah

Sebab 2 π = 360° Jadi besar dalam sudut 1 rad ialah sebagai berikut :

Pada jarak dalam waktu Δt , maka benda tersebut sudah menempuh lintasan sepanjang busur AB, dengan sudut sebesar Δθ . Oleh sebab itu, kecepatan sudut merupakan besar sudut yang ditempuh tiap satu satuan waktu. Satuan kecepatan sudut ialah rad/s . Dan Rpm ialah merupakan suatu singkatan dari rotation per minutes (rotasi per menit).

Sebab waktu yang dibutuhkanagar dapat menempuh satu putaran ialah T dan dalam satu putaran sudut yang ditempuh benda ialah 360° (2 π), maka persamaan kecepatan sudutnya ialah ω = 2 π/T Apabila telah diketahui bahwa T = 1/f atau f = 1/T sehingga persamaan kecepatan sudutnya (Z) menjadi sebagai berikut.

Atau kecepatan sudut dalam gerak melingkar juga dapat dirumuskan sebagai berikut :

Keterangan:

ω : kecepatan sudut (rad/s)

f : frekuensi (Hz)

T : periode (s)

Percepatan Sentripetal

Ialah merupakan suatu benda yang bergerak melingkar secara beraturan dan mempunyai percepatan yang disebut dengan sentripetal. Pada arah percepatan ini kerap kali menuju ke arah pusat lingkaran. Percepatan sentripetal berfungsi untuk mengubah arah kecepatan.

Percepatan sentripetal dapat ditentukan dengan penguraian arah kecepatan.

Jadi dikarenakan pada GMB besar kecepatan itu tetap, maka segitiga yang diarsir di atas merupakan segitiga sama kaki. kecepatan rata-rata dan selang waktu yang dibutuhkan untuk menempuh panjang busur AB (r) dapat ditentukan melalui persamaan berikut.

Jika kecepatan rata-rata dan selang waktu yang digunakan telah diperoleh, maka percepatan sentripetalnya adalah sebagai berikut.

Jika mendekati nol, maka persamaan percepatannya menjadi seperti berikut.

Sebab ω, jadi bentuk lain dari persamaan di atas ialah as = ω2 r. Maka, untuk benda yang melakukan GMB, percepatan sentripetalnya (as ) dapat dicari melalui persamaan berikut.

Gerak Melingkar Berubah Beraturan

Sama halnya pada pembahasan mengenai gerak lurus, karena pada gerak melingkar juga dikenal gerak melingkar berubah beraturan (GMBB). Apabila dalam perubahannya disebut percepatan searah , maka kecepatannya akan semakin meningkat. Namun apabila dalam perubahan percepatannya searah berlawanan dengan kecepatan, maka kecepatannya akan menjadi menurun.

Percepatan Total pada Gerak Melingkar Berubah Beraturan (GMB)

Pada(GMB) meski mempunyai percepatan ripetal, akan tetapi pada kecepatan linearnya tidak berubah. Mengapa? Oleh sebab sentripetal tidak dapat berguna jika merubah kecepatan linear, namun untuk mengubah arah gerak partikel sehingga lintasannya berbentuk lingkaran. Pada gerak melingkar berubah beraturan (GMBB), kecepatan linear dapat berubah secara beraturan. Besaran tersebut ialah suatu percepatan tangensial (at), yang arahnya dapat sama atau berlawanan dengan arah kecepatan linear. Percepatan sudut merupakan hasil yang didapat dari tangensial (α) kemudian dikalikan dengan jari-jari lingkaran (r). at = α’r

a_t: percepatan tangensial (m/s²)

α : percepatan sudut (rad/s²)

r : jari-jari lingkaran dalam cm atau m

Didalm GMBB terdiri dari dua percepatan yakni:

Sentripetal (a_s)
Tangensial (a_t).

Pada sentripetal yang mana ia selalu mengarah ke pusat lingkaran, namun berbeda dengan tangensial menyinggung lingkaran. Percepatan total dalam GMBB merupakan jumlah vektor dari kedua percepatan tersebut.

Dengan mengamati gambar diatas telah diketahui bahwa percepatan sentripetal dan percepatan tangensial saling tegak lurus. Oleh karena itu, percepatan totalnya ialah sebagai berikut.

Rumus Gerak Melingkar Berubah Beraturan

Rumus-rumus yang digunakan dalam GMBB tidak jauh berbeda dengan rumus-rumus dalam GLBB.

Keterangan:

ϖº = Keceptan sudut awal(rad/s)

ϖt = kecepatan sudut Akhir(rad/s)

α = Percepatan sudut (rad/s²)

t = Waktu(S)

θ = Sudut(rad)

R = jari-jari lintasan (m) Keterangan : (+) → benda mengalami percepatan

(−) → benda mengalami perlambatan.

melalui atau bersama di bawah ini : ω_t = kecepatan sudut setelah t detik (rad/s) ω_o = kecepatan sudut awal (rad/s) α = percepatan sudut (rad/s²) θ = sudut tempuh (radian) t = waktu yang diharapkan (s)

Rpm merupakan kecepatan sudut dalam satuan ppm (putaran per menit) . Satuan tersebut menyatakan banyakanya putaran yang dilakukan benda dalam satu menit. Hubungan satuan tersebut dengan rad/s yakni: 1 ppm = 1 rpm = ^π⁄₃₀ rad/s

Contoh Soal Gerak Melingkar

Contoh Soal.1 kecepatan ialah hasil bagi dari besaran panjang dan waktu. Karena kecepatan linear memiliki satuan meter/sekon maka besaran panjangnya harus bersatuan meter dan waktu bersatuan sekon. 1 putaran lingkaran berarti : jarak tempuh = Keliling lingkaran S = 2 π R (m) waktu tempuh = periode gelombang t = T (s)

sehingga kecepatan linearnya :Contoh Soal.2