Bangun Ruang Sisi Lengkung

Kumpulan Soal Bangun Ruang Sisi Lengkung Kelas Ix Matematika

Rumus Bangun Ruang Sisi Lengkung Dalam Matematika

Rumus Bangun Ruang Sisi Lengkung | Taukah anda apa yang dimaksud dengan bangun ruang sisi lengkung?dan apa sajakah yang termasuk dalam bangun ruang sisi lengkung? Dan bagaimana rumus – rumus dalam bangun sisi lengkung?Mari kita pelajari bersama.

Pengertian

Bangun ruang sisi lengkung adalah bangun ruang yang memiliki selimut dan memiliki bagian – bagian yang berupa lengkungan.

Yang termasuk dalam bangunruang sisi lengkung adalah :

1.Tabug

2.kerucut

3.Bola

Simbol – simbol yang harus di ketahui ,antara lain :

La = Luas alas

t = Tinggi

r = jari – jari lingkaran

π = terdiri dari 22/7 dan 3,14

S = garis lukis

Rumus Bangun Ruang sisi Lengkung

Tabung dianggap sebagai prisma segi takterhingga beraturan dan merupakan bangun ruang yang terdiri atas dua bidang lingkaran yang terletak di atas dan di bawah yang besarnya sama yang dihubungkan oleh dua garis lurus yang sejajar.

Perhatikan gambar dibawah ini:

Jaring – jaring tabung :

Maka rumus yang berlaku untuk bangun ruang ini adalah :

Luas alas = πr²
Luas tabung tertutup / Permukaan

= ( ka x t ) + ( 2 x La )

= ( 2rt ) + ( 2 )

= 2 ( t + r )

3. Luas tabung tanpa tutup

= ( ka x t ) + La

= 2rt +

= r ( 2t + r )

4. Volume tabung

= La x t

= πr²t

5. Luas selimut tabung

= ka x t

= 2 πrt

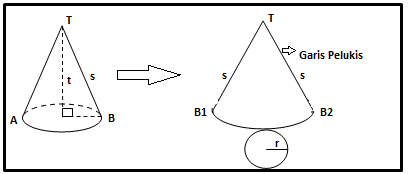
Kerucut merupakan bangun ruang sisi lengkung yang dianggap sebagai limas yang alasnya lingkaran dan memiliki garis lukis yang mengelilingi dan membentuk titik puncak.

Coba pahami gambar di bawah ini :

Dari gambar di atas maka , diketahui rumus – rumus sebagai berikut :

Volume kerucut = 1/3 x La x t

= 1/3 x πr² x t

=1/3 πr² t

Luas selimut kerucut = 2πr / 2πs x πs²

= πrs

Luas sisi kerucut = πrs + πr²

= π r ( s + r )

Hubungan s, r , dan t pada kerucut :

s² = r²+ t²

t²= s² – r²

r² = s² – t²

Bola merupakan bangun ruang sisi lengkung yang memiliki titik pusat dan dianggap sebagai kumpulan kerucut yang terdiri dari jari – jari yang sama.

Perhatikan gambar bangun ruang di bawah ini :

Dari gambar bangun ruang di atas ,dapat di dapatkan rumus – rumus sebagai berikut :

Luas Bola = 4 πr²

Luas bola benda berongga = 2πr²

Luas bola benda padat / pejal = 3πr²

Volume bola

= 1/3 La x t

= 1/3 x 4πr²x r

=4/3 πr³

jari – jari ( r )

Utuk lebih jelasnya , maka perhatika contoh – contoh berikut .

Contoh soal

Diketahui suatu tabung memiliki tinggi 20 cm ,dan jari – jarinya 28 cm. Berapakah volume tabung tersebut ?

Penyelesaian :

Diketahui : t = 20 , r = 28

Ditanyakan : V = ….????

Jawab :

V = πr²t

= 22/7 x 28² x 20

= 49280 cm³

Jadi, volume tabung tersebut adalah 49280 cm³

Diketahui luas suatu selimut tabung 616 cm² , dan tingginya 7 cm. Berapakah volume tabung tersebut?

Penyelesaian :

Diketahui : Luas selimut = 616

t = 7

Ditanya : V = …..?????

Jawab :

V = πr²t

Karena r belum di ketahui maka langkah pertama kita cari r terlebih dahulu yaitu dengan cara subsitusi dan perkalian silang ,seperti di bawah ini :

Luas selimut =2πrt

616 = 2 x22/7 x r x 7

616 x 7 = 2 x 22 x 7 x r

4312 =308 r

r = 14

Setelah r di ketahui maka kita tinggal memasukan dalam rumus volume

V = πr²t

= 22/7 x 14² x 7

=22/7 x 196 x 7

= 4312 cm³

Jadi volume tabung tersebut adalah 4312 cm³

Diketahui kerucut dengan jari – jari 5 cm dan tinggi 12 cm ,berapakah luas selimut,luas permukaan dan volume kerucut tersebut ?

Penyelesaian :

Diketahui : r = 5 , t = 12

Ditanta : a. Luas selimut = …???

Luas permukaan = ….???
volume = ….???

Jawab:

Langkah pertama yaitu mencari bagian yang belum diketahui,apakah yang belum di ketahui mari kita lihat dari rumus – rumus yang ditanyakan .

Lselimut = πrs

Lpermukaan = π r ( s + r )

Volume = 1/3 πr² t

Jadi yang di cari pertama kali adalah s = …???????

S²= r²+ t²

= 5² + 12²

= 25 + 144

= 169

S =√169

= 13

=3,14 x 5 x 13

= 204,1 cm²

Luas Permukaan = π r ( s + r )

= 3,14 x 5 ( 13 + 5 )

= 15,7 x 18

= 282,6 cm²

= 1/3 x 3,14 x 5 x 5 x 12

= 314 cm³

Suatu bola memiliki volume 381,51 cm³, hitunglah jari – jari bola tersebut !

Penyelesaian :

Diketahui : v bola = 381,51

Ditanya : r = …???

Jawab

V = 4/3 πr³

381,51 =4/3 x 3,14 x r³

r³= ( 381,51 x 3 ) : ( 4 x 3,14 )

=91,125

r = 4,5 cm

Perhatikan gambar dibawah ini ,

Apabila jari jarinya 7 cm dan tingginya 24, maka hitunglah:

Volumenya
Apabila 1cm³beratnya 12 gr maka ,hitunglah berat benda tersebut !
Luas permukaan benda tersebut

Penyelesaian :

Diketahui : r = 7 , t = 24

Jawab :

Volume benda = V kerucut + V setengah bola

= 1/3 πr² t + 2/3 πr³

=1/3 x 22/7 x 7 x 7 x 24 + 2/3 x 22/7 x 7 x 7 x 7

= 1232 + 718,67

= 1950,67 cm³

2. Berat benda = 1950,67 x 12 gr

= 23408,04 gr

= 23,40804 kg

3. s = √7² + 24²

= √49 + 576

=√ 625

= 25

Lselimut = π rs

=22/7 x 7 x 25

= 550 cm²

L setengah bola berongga = 2πr²

= 2 x 22/7 x 7 x 7

= 308 cm²

Lpermukaan benda = Lsel + Lsetbola

= 550 + 308

= 858 cm²

Demikian penjelasan mengenai Macam – macam dan Rumus Bangun Ruang sisi lengkung . Dalam menyelesaikan soal bangun ruang sisi lengkung itu mudah , cuma kita harus faham dengan rumus – ruusnya , jangan sampai tertukar antara bangun ruang yang satu dengan yang lainnya . Karena rumusnya hampir sama . Semoga bermanfaat