Sistem Persamaan Linear Dua Variabel

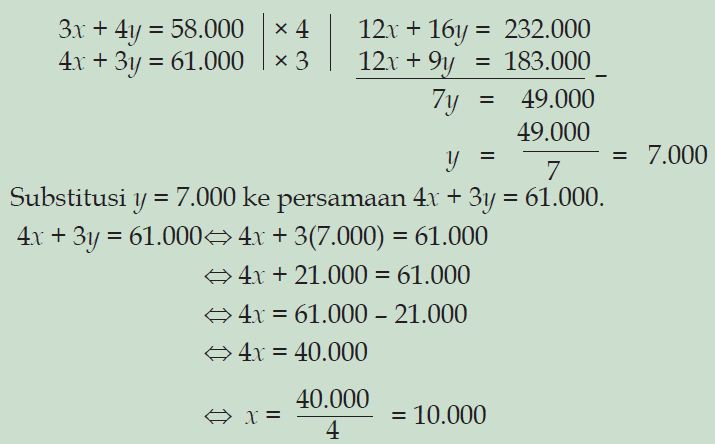Cara Menyelesaikan Soal Cerita Yang Berhubungan Dengan

Soal Persamaan Linear Dua Variabel (SPLDV) plus Kunci Jawaban

Halo adik-adik, berikut ini kakak admin bagikan contoh Soal Persamaan Linear Dua Variabel (SPLDV), Soal Matematika Kelas 8 SMP lengkap dengan Kunci Jawaban dan Pembahasan.

Soal Persamaan Linear Dua Variabel (SPLDV) ini terdiri dari 25 butir soal pilihan ganda yang bisa adik-adik pelajari langsung di sini. Selain dari pada itu, kalian juga bisa mendownload soal ini untuk tambahan referensi belajar di rumah. Semoga contoh Soal Persamaan Linear Dua Variabel (SPLDV) dengan kunci jawaban dan pembahasan ini bermanfaat untuk adik-adik khususnya yang sudah kelas 8 Sekolah Menengah Pertama (SMP/ SLTP/MTs). Ok, selamat belajar ....

I. Berilah tanda silang (X) pada huruf a, b, c atau d di depan jawaban yang paling benar !

1. Perhatikan persamaan-persamaan berikut ! (i) 3p + 5q = 10 (II) 2x2 - 3y = 6 (III) 3y = 5x – 2 (IV) 3x + 5 = 2x – 3y Yang bukan merupakan persamaan linear dua variabel adalah .... a. (i) b. (II) c. (III) d. (IV)

Pembahasan:

(i) 3p + 5q = 10 : merupakan PLDV karena terdapat variabel p dan q (II) 2x2 - 3y = 6 : bukan PLDV karena 2x2 merupakan bagian dari persamaan kuadrat bukan persamaan linear (III) 3y = 5x – 2 : merupakan PLDV karena terdapat variabel x dan y (IV) 3x + 5 = 2x – 3y : merupakan PLDV karena terdapat variabel x dan y

Jawaban: b

2. Perhatikan persamaan-persamaan berikut ! (i) 15 – 5x = 23 (II) 5x = 20 – 3y (III) x2 - y2 = 49 (IV) 3x2 + 6x + 12 = 0 Yang merupakan persamaan linear dua variabel adalah .... a. (I) b. (II) c. (III) d. (IV)

Pembahasan:

(i) 15 – 5x = 23 : bukan PLDV karena hanya terdapat satu variabel (II) 5x = 20 – 3y : merupakan PLDV kkarena terdapat variabel x dan y (III) x2 - y2 = 49 : bukan PLDV karena x2 dan y2 merupakan bagian dari persamaan kuadrat bukan persamaan linear (IV) 3x2 + 6x + 12 = 0 : bukan PLDV karena terdapat 3x2 merupakan bagian dari persamaan kuadrat bukan persamaan linear

Jawaban: b

3. Rina membeli 3 kg apel dan 2 kg jeruk. Uang yag harus dibayarkan adalah Rp 65.000,00. Jika diubah menjadi persamaan linear dua variabel, maka pernyataan tersebut menjadi .... a. 3x + 2y = 65.000 b. 3x – 2y = 65.000 c. 3x + 2y = 65 d. 3x – 2y = 65

Pembahasan:

Misal x = apel Y = jeruk Harga 3 kg apel dan 2 kg jeruk = 65.000 Jika dijadikan persamaan linear dua variabel adalah 3x +2y = 65.000

Jawaban: a

4. Seorang pedagang menjual 3 buah pensil dan 5 buah buku seharga Rp 19.500,00. Jika diubah menjadi persamaan linear dua variabel, maka pernyataan tersebut menjadi .... a. 3x - 5y = 19.5 b. 3x + 5y = 19.500 c. 3x - 5y = 19.5 d. 3x + 5y = 19.500

Pembahasan :

Misal x = pensil Y = buku Harga 3 buah pensil dan 5 buah buku adalah 19.500 Jika dijadikan persamaan linear dua variabel adalah 3x + 5y = 19.500

Jawaban : d

5. Keliling sebuah persegi panjang adalah 64 cm. Jika diubah menjadi persamaan linear dua variabel, maka pernyataan tersebut menjadi .... a. 2p – 2l = 64 b. p x l = 64 c. 2p + 2l = 64 d. p + l = 64

Pembahasan :

Rumus keliling persegi panjang = (2 x panjang) + (2 x lebar) Missal p = panjang l = lebar Bentuk persamaan linear akan menjadi : 2p + 2l =64

Jawaban : c

6. Himpunan penyelesaian dari sistem persamaan x + y = 12, x – y = 4 adalah .... a. { 4 , 8 } b. { 12 , 4 } c. { 4 , 12 } d. { 8 , 4 }

7. Himpunan penyelesaian dari sistem persamaan x - y = 6, x + y = 10 adalah .... a. {8 , 2} b. {2 , 8} c. {6 , 10} d. {10 , 6}

8. Himpunan penyelesaian dari sistem persamaan 2x - 5y = 1, 4x – 3y = 9 adalah .... a. {1, 3 } b. {2, 5 } c. {3, 1 } d. {4, 3 }

9. Himpunan penyelesaian dari sistem persamaan 2x - y = 4, -2x – 3y = -4 adalah .... a. {4 , -4} b. {2 , 0} c. {2 , 3} d. {2 , -2}

10. Himpunan penyelesaian dari sistem persamaan 4x = 5y, 3y = 7 – 5x adalah .... a. {-35/13 , -28/13} b. {28/13, 35/13} c. {-28/13, -35/13} d. {35/13 , 28/13}

11. Himpunan penyelesaian dari sistem persamaan y = 2x, 6x – y = 8 adalah .... a. {2,6} b. {2,8} c. {2,2} d. {2,4}

Pembahasan : metode substitusi

y = 2x ……………………..I 6x – y = 8………………..II Substitusikan persamaan I ke dalam persamaan II sehingga diperoleh 6x – (2x) = 8 4x = 8 X = 8/4 X = 2 Substitusikan x=2 pada persamaan II sehingga diperoleh y = 2x y = 2 (2) y = 4 Jadi himpunan penyelesaian dari persamaan di atas adalah {2,4}

Jawaban : d

12. Himpunan penyelesaian dari sistem persamaan x = 2y + 9, x + 5y + 5 = 5 adalah .... a. {2,9} b. {135/31 , -9/7} c. {5,5} d. {9,5}

Pembahasan : metode substitusi

x = 2y + 9……………………….I x + 5y + 5 = 5……………….II Substitusikan persamaan I ke dalam persamaan II sehingga diperoleh (2y + 9) + 5y + 5 = 5 7y + 14 = 5 7y = 5 – 14 7y = -9 y = -9/7 Substitusikan y = -9/7 pada persamaan II sehingga diperoleh x = 2 (-9/7) + 9 x = -18 /7 + 9 x = -162/63 + 567/63 x = 405/63 x = 135/31 Jadi himpunan penyelesaian dari persamaan di atas adalah {135/31 , -9/7}

Jawaban : b

13. Himpunan penyelesaian dari sistem persamaan 2x + y = 0, 7x + 5y =1 adalah .... a. {-1/3 , -2/3} b. {-1/3 , 2/3} c. {1/3 , 2/3} d. {1/3 , -2/3}

Pembahasan : metode substitusi

2x + y = 0 => y = -2x ……………….I 7x + 5y =1…………………………………..II Substitusikan persamaan I ke dalam persamaan II sehingga diperoleh 7x + 5(-2x) =1 7x -10x = 1 -3x = 1 x = -1/3 Substitusikan x = -1/3 pada persamaan II sehingga diperoleh 2(-1/3) + y = 0 -2/3 + y =0 y = 2/3 Jadi himpunan penyelesaian dari persamaan di atas adalah {-1/3 , 2/3}

Jawaban : b

14. Himpunan penyelesaian dari sistem persamaan 6u – v = 1, 4u – 3v + 4 = 0 adalah .... a. {-1/2 , 2} b. {1/2 , -2} c. {1/2 , 2} d. {-1/2 , -2}

Pembahasan : metode substitusi

6u – v = 1 => 6u – 1 = v………………I 4u – 3v + 4 = 0……………………………….II Substitusikan persamaan I ke dalam persamaan II sehingga diperoleh 4u – 3(6u – 1) + 4 = 0 4u - 18u + 3 + 4= 0 -14u +7 = 0 -14u = -7 U = -7/-14 U = ½ Substitusikan u = ½ pada persamaan II sehingga diperoleh 6 (1/2) – v = 1 3 – v = 1 -v = 1 – 3 -v = -2 v = 2 Jadi himpunan penyelesaian dari persamaan di atas adalah {1/2 , 2}

Jawaban : c

15. Himpunan penyelesaian dari sistem persamaan 5p + q = 10, 14p + 3q = 18 adalah .... a. {12 , -50} b. {1, 2} c. {18, -10} d. {14, 3}

Pembahasan : metode substitusi

5p + q = 10 => q = 10 – 5p…………………….I 14p + 3q = 18…………………………………………..II Substitusikan persamaan I ke dalam persamaan II sehingga diperoleh 14p + 3 ( 10 – 5p) = 18 14p + 30 -15p = 18 -p = 18 – 30 -p = -12 P = 12 Substitusikan P = 12 pada persamaan II sehingga diperoleh q = 10 – 5p q = 10 – 5 (12) q = 10 – 60 q = -50 Jadi himpunan penyelesaian dari persamaan di atas adalah {12 , -50}

Jawaban : a

16. Salah satu himpunan penyelesaian dari persamaan 3x – 2y = -18 adalah .... a. {-6, 9} b. {2, -12} c. {4, 15} d. {0, -9}

Pembahasan : metode termudah

3 (-6) – 2(9) = -18 -18 -16 = -18 -34 = -18 3 (2) – 2(-12) = -18 6 + 24 = -18 30 = -18 3 (4) – 2(15) = -18 12 – 30 = -18 -18 = -18 3 (0) – 2 (-9) = -18 0 + 18 = -18

Jawaban : c

17.

Grafik di atas merupakan himpunan penyelesaian dari persamaan .... a. 2x + y = 6, x, y = є R b. 2x - y = 6, x, y = є R c. -2x + y = 6, x, y = є R d. -2x - y = 6, x, y = є R

Pembahasan :

(3 , 0 ) dan (0 , 6) Jawaban a. 2x + y = 6, x, y = є R Ketika x = 3 dan y = 0 2x + y = 6 2 (3) + 0 = 6 6 = 6 (sama) Ketika x = 0 dan y = 6 2x + y = 6 2 (0) + 6 = 6 6 = 6 (sama) Jadi persamaan dari grafik di atas adalah 2x + y =6

Jawaban : a

18. Persamaan yang ekuivalen dengan x – y = 5 adalah .... a. 2x + 2y = 5 b. 2x + 2y = 10 c. 2x – 2y = 10 d. 2x – 2y = 5

Pembahasan :

2x – 2y = 10 (dibagi 2) X – y = 5

Jawaban : c

19. Penyelesaian dari sistem persamaan x – 2y = 3 dan 5x – 2y = -1 adalah .... a. x = -1 dan y = -2 b. x = -2 dan y = -1 c. x = 1 dan y = -2 d. x = -1 dan y = 2

Pembahasan : Metode Substitusi

x – 2y = 3 => x = 3 + 2y…………………..I 5 x – 2y = -1………………………………………II Substitusikan persamaan I ke dalam persamaan II sehingga diperoleh 5 ( 3 + 2y) – 2y = -1 15 + 10y – 2y = -1 8y = -1 – 15 8y = -16 y = -16 / 8 y = -2 Substitusikan y = -2 pada persamaan I sehingga diperoleh x = 3 + 2 (-2) x = 3 – 4 x = -1 Jadi nilai x = -1 dan nilai y = -2

Jawaban : a

20. Jika diketahui x = 2 dan y = 3 dalam persamaan px + qy = 5 dan px – qy = 3, maka .... a. p = -2 dan q = 1/3 b. p = 2 dan q = ―1/3 c. p = 2 dan q = 1/3 d. p = -2 dan q = ―1/3

21. Diketahui sistem persamaan 3x + 2y = 8; x – 5y = ― 37. Nilai 6x + 4y adalah .... a. ―30 b. ―16 c. 16 d. 30

Pembahasan :

3x + 2y = 8 3 (-37 + 5y) + 2y = 8 -111 + 15y + 2y = 8 17y = 119 Y =7 X = -37 + 5 (7) X = -37 +35 X = -2 Nilai 6 x + 4y = 6 (-2) + 4 (7) = -12 + 28 = 16

Jawaban : c

22. Jika x = 2y disubstitusikan pada persamaan x + y = ―6 maka himpunan penyelesaiannya adalah .... a. {-8, -2} b. {-2, -4} c. {-4, -2} d. {26, 24}

Pembahasan : metode termudah

2y + y = -6 3y = -6 y = -6 /3 y = -2 x = 2y x = 2 (-2) x = -4

Jawaban : c

23. Harga 4 buah donat dan 5 buah roti kukus adalah Rp 4.550,00. Sedangkan harga 2 buah donat dan 3 buah roti kukus adalah Rp 2.550,00. Harga 1 buah donat dan 2 buah roti kukus adalah .... a. Rp 450,00 dan Rp 550,00 b. Rp 550,00 dan Rp 450,00 c. Rp 450,00 dan Rp 1.100,00 d. Rp 1.100,00 dan Rp 450,00

24. Persamaan berikut yang grafiknya melalui titik (1,2) adalah .... a. x + 2y = 5 b. x + y = 2 c. 2x + y = 2 d. 2x + 2y = 5

Pembahasan :

x = 1 y = 2 x + 2y = 5 => x + 2y = 1 + 2 (2) = 5 x + y = 2 => x + y = 1 + 2 = 3 2x + y = 2 => 2x + y = 2(1) + 2 =4 2x + 2y = 5 => 2x + 2y = 2(1) + 2(2) = 6

Jawaban : a

25. Harga 8 buah buku tulis dan 6 buah pensil Rp 14.400,00. Harga 6 buah buku tulis dan 5 buah pensil Rp 11.200,00. Jumlah harga 5 buah buku tulis dan 8 buah pensil adalah .... a. Rp 11.800,00 b. Rp 14.800,00 c. Rp 12.800,00 d. Rp 13.600,00

Untuk lebih jelasnya, berikut ini file soal dalam bentuk PDF yang bisa didownload ⇩

Soal Persamaan Linear Dua Variabel (SPLDV) plus Kunci Jawaban dan Pembahasan 

Soal Persamaan Linear Dua Variabel (SPLDV) plus Kunci Jawaban adalah konten yang disusun oleh Juragan Les dan dilindungi undang-undang hak cipta. Dilarang mengcopy paste dan mempublish ulang konten dalam bentuk apapun ! Terima kasih

Itulah 25 Contoh Soal Persamaan Linear Dua Variabel (SPLDV) plus Kunci Jawaban. Semoga bermanfaat untuk menambah referensi belajar.

Gallery Sistem Persamaan Linear Dua Variabel

Metode Penyelesaian Sistem Persamaan Linier Dua Variabel

Contoh Soal Eliminasi 3 Variabel Pecahan Kumpulan Soal

Persamaan Linear Dua Variabel Matematika Kelas 10

Sistem Persamaan Linear Dua Dan Tiga Variabel Docx

Pdf Pengembangan Lks Dengan Pendekatan Realistik Pada

Sistem Persamaan Linier Dua Variabel

Judul Situs

Sistem Persamaan Linear Dua Variabel Spldv Pembelajaran

Belajar Sistem Persamaan Linear Dua Variabel

Sistem Persamaan Linear Dua Dan Tiga Variabel Docx

Sistem Persamaan Linear Dua Variabel Geogebra

Sistem Persamaan Linear Dan Pertidaksamaan Dua Variabel

Persamaan Linear Lessons Tes Teach

Pengertian Dan Metode Penyelesaian Spldv Secara Lengkap

Sistem Persamaan Linear Tiga Variabel Geogebra

Persamaan Linear Dua Variabel

Spldv Qvndjvpr9jnx

Sistem Persamaan Linear Tiga Variabel

Doc Sistem Persamaan Linear Dua Variabel Ray Asfara

Share this post