Fluida Statis Dan Dinamis

E Modul Fluida Statis For Android Apk Download

Pengertian Fluida Statis dan Dinamis, Massa Jenis, Tekanan Hidrostatis Total, Aplikasi, Tegangan Permukaan, Rumus, Contoh Soal, Kunci Jawaban

Pengertian Fluida Statis dan Dinamis, Massa Jenis, Tekanan Hidrostatis Total, Aplikasi, Tegangan Permukaan, Rumus, Contoh Soal, Kunci Jawaban - Perhatikanlah serangga yang sedang diam di atas permukaan air. Mengapa serangga tersebut dapat berdiri di atas permukaan air? Bagaimanakah hukum Fisika menerangkan peristiwa ini? Peristiwa serangga yang sedang berdiam diri di atas permukaan air seperti pada gambar, berhubungan dengan salah satu sifat air sebagai fluida, yaitu tegangan permukaan. Oleh karena adanya tegangan permukaan zat cair, serangga dan benda-benda kecil lainnya dapat terapung di atas permukaan air. Fluida, yaitu zat cair dan gas telah memberikan banyak manfaat bagi manusia karena keistimewaan sifat yang dimilikinya. Kemudahan transportasi air dan udara merupakan salah satu contoh aplikasi teknologi yang berkaitan dengan sifat fluida. Tahukah Anda sifat-sifat fluida lainnya dan aplikasinya dalam kehidupan sehari-hari? Pada Bab ini, Anda akan mendalami pembahasan mengenai fluida yang ditinjau dari keadaan statis dan dinamisnya.

Serangga berjalan di atas air. [1]

Fluida adalah zat yang dapat mengalir dan berubah bentuk (dapat dimampatkan) jika diberi tekanan. Jadi, yang termasuk ke dalam fluida adalah zat cair dan gas. Perbedaan antara zat cair dan gas terletak pada kompresibilitasnya atau ketermampatannya. Gas mudah dimampatkan, sedangkan zat cair tidak dapat dimampatkan. Ditinjau dari keadaan fisisnya, fluida terdiri atas fluida statis atau hidrostatika, yaitu ilmu yang mempelajari tentang fluida atau zat alir yang diam (tidak bergerak) dan fluida dinamis atau hidrodinamika, yaitu ilmu yang mempelajari tentang zat alir atau fluida yang bergerak. Hidrodinamika yang khusus membahas mengenai aliran gas dan udara disebut aerodinamika.

Sifat fisis fluida dapat ditentukan dan dipahami lebih jelas saat fluida berada dalam keadaan diam (statis). Sifat-sifat fisis fluida statis yang akan dibahas pada subbab ini di antaranya, massa jenis, tekanan, tegangan permukaan, kapilaritas, dan viskositas. Bahasan mengenai massa jenis dan tekanan telah Anda pelajari di SMP sehingga uraian materi yang disajikan dalam subbab ini hanya bertujuan mengingatkan Anda tentang materi tersebut. Catatan Fisika :

Ikan Tulang Keras

Guiyu oneiros, Bony fish. [2]

Ikan tulang (bony fishes) memiliki kantung udara di dalam tubuhnya yang berfungsi sebagai pelampung renang. Agar dapat tetap melayang di dalam air, tekanan udara dalam kantung diatur menurut kedalaman air. Dengan menekan udara dalam kantung tersebut, tulang ikan dapat turun lebih dalam lagi. (Sumber: Jendela Iptek, 1997)

1. Massa Jenis

Pernahkah Anda membandingkan berat antara kayu dan besi? Benarkah pernyataan bahwa besi lebih berat daripada kayu? Pernyataan tersebut tentunya kurang tepat, karena segelondong kayu yang besar jauh lebih berat daripada sebuah bola besi. Pernyataan yang tepat untuk perbandingan antara kayu dan besi tersebut, yaitu besi lebih padat daripada kayu.

Anda tentu masih ingat, bahwa setiap benda memiliki kerapatan massa yang berbeda-beda serta merupakan sifat alami dari benda tersebut. Dalam Fisika, ukuran kepadatan (densitas) benda homogen disebut massa jenis, yaitu massa per satuan volume. Secara matematis, massa jenis dituliskan sebagai berikut.

ρ = m / V (1-1)

dengan:

m = massa (kg atau g),

V = volume (m³ atau cm³), dan

ρ = massa jenis (kg/m³ atau g/cm³)

Jenis beberapa bahan dan massa jenisnya dapat dilihat pada Tabel 1. berikut.

Tabel 1. Massa Jenis atau Kerapatan Massa (Density)

Bahan	Massa Jenis (g/cm³)	Nama Bahan	Massa Jenis (g/cm³)
Air	1,00	Gliserin	1,26
Aluminium	2,7	Kuningan	8,6
Baja	7,8	Perak	10,5
Benzena	0,9	Platina	21,4
Besi	7,8	Raksa	13,6
Emas	19,3	Tembaga	8,9
Es	0,92	Timah Hitam	11,3
Etil Alkohol	0,81
Sumber : College Physics, 1980

2. Tekanan Hidrostatis

Masih ingatkah Anda definisi tekanan? Tekanan adalah gaya yang bekerja tegak lurus pada suatu permukaan bidang dan dibagi luas permukaan bidang tersebut. Secara matematis, persamaan tekanan dituliskan sebagai berikut.

p = F / A (1-2)

dengan:

F = gaya (N),

A = luas permukaan (m²), dan

p = tekanan (N/m² = Pascal).

Persamaan (1–2) menyatakan bahwa tekanan p berbanding terbalik dengan luas permukaan bidang tempat gaya bekerja. Jadi, untuk besar gaya yang sama, luas bidang yang kecil akan mendapatkan tekanan yang lebih besar daripada luas bidang yang besar. Dapatkah Anda memberikan beberapa contoh penerapan konsep tekanan dalam kehidupan sehari-hari?

Tekanan hidrostatis disebabkan oleh fluida tak bergerak. Tekanan hidrostatis yang dialami oleh suatu titik di dalam fluida diakibatkan oleh gaya berat fluida yang berada di atas titik tersebut. Perhatikanlah Gambar 1.

Gambar 1. Dasar bejana yang terisi dengan fluida setinggi h akan mengalami tekanan hidrostatis sebesar p.

Jika besarnya tekanan hidrostatis pada dasar tabung adalah p, menurut konsep tekanan, besarnya p dapat dihitung dari perbandingan antara gaya berat fluida (F) dan luas permukaan bejana (A).

p = F / A = gaya berat fluida / luas permukaan bejana

Gaya berat fluida merupakan perkalian antara massa fluida dengan p = (m_fluida x g) / A. Oleh karena m = ρV, persamaan tekanan oleh fluida dituliskan sebagai p = ρVg / A.

Volume fluida di dalam bejana merupakan hasil perkalian antara luas permukaan bejana (A) dan tinggi fluida dalam bejana (h). Oleh karena itu, persamaan tekanan di dasar bejana akibat fluida setinggi h dapat dituliskan menjadi :

p = ρ (Ah)g / A = ρhg

Jika tekanan hidrostatis dilambangkan dengan ph, persamaannya dituliskan sebagai berikut.

p_h = ρ gh (1–3)

dengan:

ph = tekanan hidrostatis (N/m²),

ρ = massa jenis fluida (kg/m³),

g = percepatan gravitasi (m/s²), dan

h = kedalaman titik dari permukaan fluida (m).

Semakin tinggi dari permukaan Bumi, tekanan udara akan semakin berkurang. Sebaliknya, semakin dalam Anda menyelam dari permukaan laut atau danau, tekanan hidrostatis akan semakin bertambah. Mengapa demikian? Hal tersebut disebabkan oleh gaya berat yang dihasilkan oleh udara dan zat cair. Anda telah mengetahui bahwa lapisan udara akan semakin tipis seiring bertambahnya ketinggian dari permukaan Bumi sehingga tekanan udara akan berkurang jika ketinggian bertambah. Adapun untuk zat cair, massanya akan semakin besar seiring dengan bertambahnya kedalaman. Oleh karena itu, tekanan hidrostatis akan bertambah jika kedalaman bertambah.

Contoh Soal 1 :

Tabung setinggi 30 cm diisi penuh dengan fluida. Tentukanlah tekanan hidrostatis pada dasar tabung, jika g = 10 m/s² dan tabung berisi:

a. air,

b. raksa, dan

c. gliserin.

Gunakan data massa jenis pada Tabel 7.1.

Kunci Jawaban :

Diketahui: h = 30 cm dan g = 10 m/s².

a. Tekanan hidrostatis pada dasar tabung yang berisi air:

P_h = ρ gh = (1.000 kg/m³) (10 m/s²) (0,3 m) = 3.000 N/m²

b. Tekanan hidrostatis pada dasar tabung yang berisi air raksa:

P_h = ρ gh = (13.600 kg/m³) (10 m/s²) (0,3 m) = 40.800 N/m²

c. Tekanan hidrostatis pada dasar tabung yang berisi gliserin:

P_h = ρ gh = (1.260 kg/m³) (10 m/s²) (0,3 m) = 3.780 N/m²

Perhatikan Gambar 2.

Gambar 2. Semakin dalam kedudukan sebuah titik dalam fluida, tekanan hidrostatis di titik tersebut akan semakin besar.

Pada gambar tersebut, tekanan hidrostatis di titik A, B, dan C berbeda-beda. Tekanan hidrostatis paling besar adalah di titik C. Dapatkah Anda menjelaskan alasannya?

Prinsip tekanan hidrostatis ini digunakan pada alat-alat pengukur tekanan. Alat-alat pengukur tekanan yang digunakan untuk mengukur tekanan gas, di antaranya sebagai berikut.

a. Manometer Pipa Terbuka

Manometer pipa terbuka adalah alat pengukur tekanan gas yang paling sederhana. Alat ini berupa pipa berbentuk U yang berisi zat cair. Perhatikan Gambar 3.

Gambar 3. Manometer pipa terbuka. [3]

Ujung yang satu mendapat tekanan sebesar p (dari gas yang hendak diukur tekanannya) dan ujung lainnya berhubungan dengan tekanan atmosfir (p0).

Besarnya tekanan udara di titik y₁ = p₀, sedangkan tekanan udara di titik y₂ = p. y₁ memiliki selisih ketinggian Δy₁ = 0 dan y₂ memiliki selisih ketinggian Δy₂ =h. Berdasarkan Persamaan (1–3) tentang besar tekanan hidrostatik, besarnya tekanan udara dalam tabung pada Gambar 3. dinyatakan dengan persamaan berikut ini.

p_gas = p – p₀ = ρ gh (1–4)

dengan ρ = massa jenis zat cair dalam tabung.

b. Barometer

Barometer raksa ini ditemukan pada 1643 oleh Evangelista Torricelli, seorang ahli Fisika dan Matematika dari Italia.

Gambar 4. Skema barometer raksa.

Ia mendefinisikan tekanan atmosfir dalam bukunya yang berjudul "A Unit of Measurement, The Torr" Tekanan atmosfer (1 atm) sama dengan tekanan hidrostatis raksa (mercury) yang tingginya 760 mm. Cara mengonversikan satuannya adalah sebagai berikut.

ρ raksa × percepatan gravitasi Bumi × panjang raksa dalam tabung

atau

(13.600 kg/cm³)(9,8 m/s²)(0,76 m) = 1,103 × 105 N/m²

Jadi,

1 atm = 76 cmHg = 1,013 × 105 N/m² (1–5)

c. Pengukur Tekanan Ban

Alat ini digunakan untuk mengukur tekanan udara di dalam ban. Bentuknya berupa silinder panjang yang di dalamnya terdapat pegas. Saat ujungnya ditekankan pada pentil ban, tekanan udara dari dalam ban akan masuk ke dalam silinder dan menekan pegas. Besarnya tekanan yang diterima oleh pegas akan diteruskan ke ujung lain dari silinder yang dihubungkan dengan skala. Skala ini telah dikalibrasi sehingga dapat menunjukkan nilai selisih tekanan udara luar (atmosfer) dengan tekanan udara dalam ban.

Gambar 5. Alat pengukur tekanan udara di dalam ban.

3. Tekanan Total

Tinjaulah sebuah tabung yang diisi dengan fluida setinggi h, seperti tampak pada Gambar 6.

Gambar 6. Tekanan total atau tekanan mutlak yang dialami oleh titik A yang berada di dalam suatu fluida adalah sebesar p_A.

Pada permukaan fluida yang terkena udara luar, bekerja tekanan udara luar yang dinyatakan dengan p. Jika tekanan udara luar ikut diperhitungkan, besarnya tekanan total atau tekanan mutlak pada satu titik di dalam fluida adalah

p_A = p₀ + ρ gh (1–6)

dengan:

p₀ = tekanan udara luar = 1,013 × 105 N/m², dan

p_A = tekanan total di titik A (tekanan mutlak).

Contoh Soal 2 :

Jika diketahui tekanan udara luar 1 atm dan g = 10 m/s², tentukanlah tekanan total di bawah permukaan danau pada kedalaman:

a. 10 cm,

b. 20 cm, dan

c. 30 cm.

Kunci Jawaban :

Diketahui: p₀ = 1 atm dan g = 10 m/s².

a. Tekanan total di bawah permukaan danau pada kedalaman 10 cm:

p_A = p₀ + ρgh = (1,013 × 10⁵ N/m²) + (1.000 kg/m³) (10 m/s²) (0,1 m)

p_A= 1,023 × 10⁵ N/m²

b. Tekanan total di bawah permukaan danau pada kedalaman 20 cm:

p_A = p₀ + ρgh = (1,013 × 10⁵ N/m²) + (1.000 kg/m³) (10 m/s²) (0,2 m)

p_A = 1,033.10⁵ N/m²

c. Tekanan total di bawah permukaan danau pada kedalaman 30 cm:

p_A = p₀ + ρgh = (1,013 × 10⁵ N/m²) + (1.000 kg/m³) (10 m/s²) (0,3 m)

p_A = 1,043.10⁵ N/m²

4. Hukum Utama Hidrostatis

Perhatikanlah Gambar 7.

Gambar 7. Tekanan di titik A, B, C, dan D sama besar, serta tidak bergantung pada bentuk penampang tempat fluida tersebut.

Gambar tersebut memperlihatkan sebuah bejana berhubungan yang diisi dengan fluida, misalnya air. Anda dapat melihat bahwa tinggi permukaan air di setiap tabung adalah sama, walaupun bentuk setiap tabung berbeda. Bagaimanakah tekanan yang dialami oleh suatu titik di setiap tabung? Samakah tekanan total di titik A, B, C, dan D yang letaknya segaris? Untuk menjawab pertanyaan tersebut, Anda harus mengetahui Hukum Utama Hidrostatis.

Hukum Utama Hidrostatis menyatakan bahwa semua titik yang berada pada bidang datar yang sama dalam fluida homogen, memiliki tekanan total yang sama. Jadi, walaupun bentuk penampang tabung berbeda, besarnya tekanan total di titik A, B, C, dan D adalah sama.

Persamaan Hukum Utama Hidrostatis dapat diturunkan dengan memperhatikan Gambar 8.

Gambar 8. Tekanan total di titik A dan B pada bejana U yang terisi fluida homogen adalah sama besar, pA = pB.

Misalkan, pada suatu bejana berhubungan dimasukkan dua jenis fluida yang massa jenisnya berbeda, yaitu ρ₁ dan ρ₂.

Jika diukur dari bidang batas terendah antara fluida 1 dan fluida 2, yaitu titik B dan titik A, fluida 2 memiliki ketinggian h₂ dan fluida 1 memiliki ketinggian h₁.

Tekanan total di titik A dan titik B sama besar. Menurut persamaan tekanan hidrostatis, besarnya tekanan di titik A dan titik B bergantung pada massa jenis fluida dan ketinggian fluida di dalam tabung. Secara matematis, persamaannya dapat dituliskan sebagai berikut.

p_A = p_B

p₀ + ρ₁gh₁ = p₀ + ρ₂gh₂

ρ₁h₁= ρ₂h₂ (1–7)

dengan:

h₁ = jarak titik A terhadap permukaan fluida 1,

h₂ = jarak titik B terhadap permukaan fluida 2,

ρ₁ = massa jenis fluida satu, dan

ρ₂ = massa jenis fluida dua.

Contoh Soal 3 :

Perhatikanlah gambar bejana di bawah ini.

Jika diketahui massa jenis minyak 0,8 g/cm³, massa jenis raksa 13,6 g/cm³, dan massa jenis air 1 g/cm³, tentukanlah perbedaan tinggi permukaan antara minyak dan air.

Kunci Jawaban :

Diketahui: ρ_m = 0,8 g/cm³, ρ_r = 13,6, dan ρ_air = 1 g/cm³.

ρ_ah_a = ρ_mh_m → h_a = (ρ_m / ρ_a) h_m = (0,8 g/cm³) / (1 g/cm³) x 15 cm³ = 12 cm.

Jadi, perbedaan tinggi permukaan minyak dan air = 15 cm – 12 cm = 3 cm.

Tokoh Fisika :

Blaise Pascal

Blaise Pascal. [4]

Blaise Pascal lahir di Clermont-Ferrand, Prancis. Ia dikenal sebagai seorang matematikawan dan fisikawan yang handal. Penelitiannya dalam ilmu Fisika, membuat ia berhasil menemukan barometer, mesin hidrolik dan jarum suntik. (Sumber: www.all iographies.com)

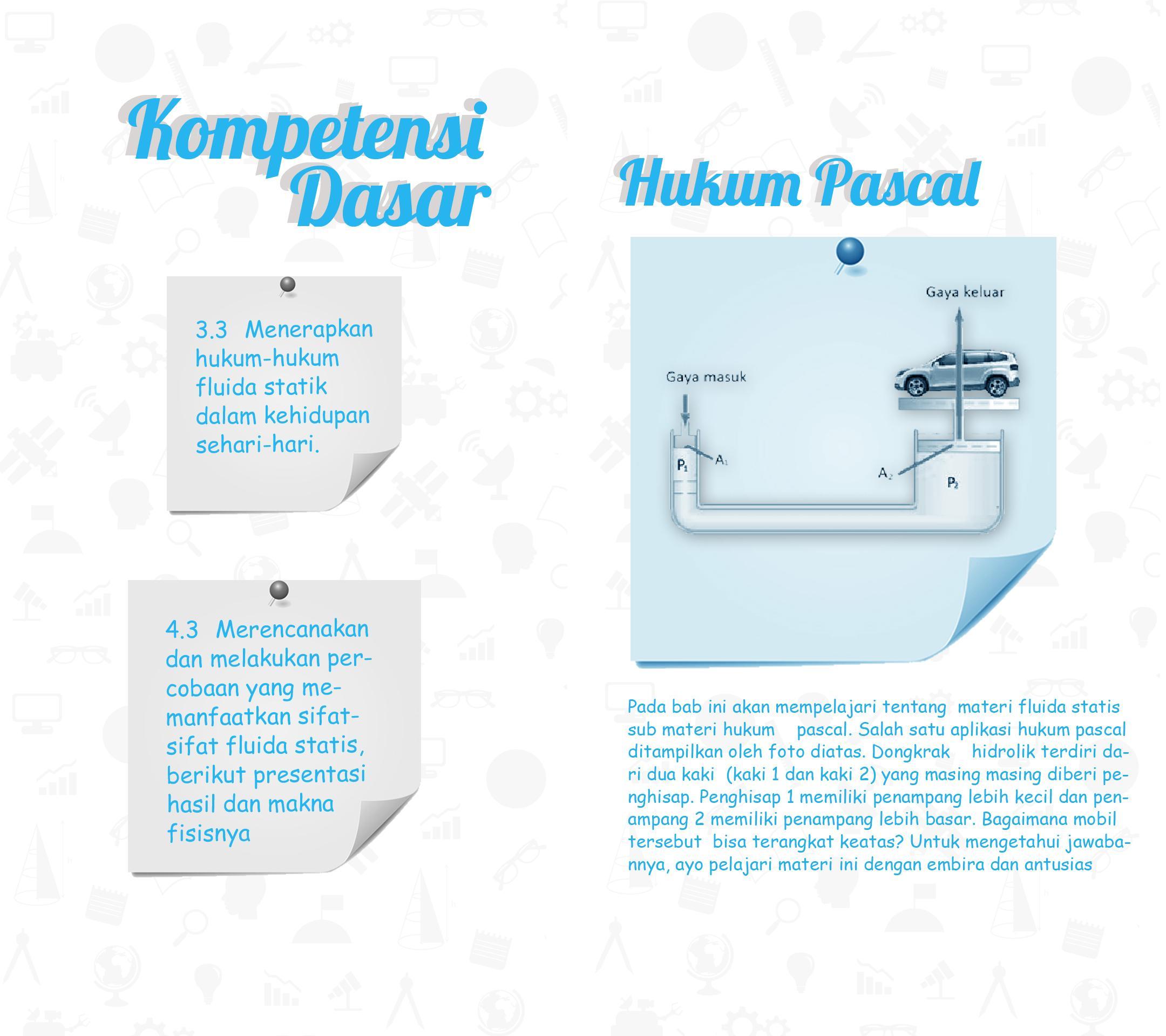
5. Hukum Pascal

Bagaimana jika sebuah bejana U diisi dengan fluida homogen dan salah satu pipanya ditekan dengan gaya sebesar F? Proses Fisika yang terjadi pada bejana U seperti itu diselidiki oleh Blaise Pascal. Melalui penelitiannya, Pascal berkesimpulan bahwa apabila tekanan diberikan pada fluida yang memenuhi sebuah ruangan tertutup, tekanan tersebut akan diteruskan oleh fluida tersebut ke segala arah dengan besar yang sama tanpa mengalami pengurangan. Pernyataan ini dikenal sebagai Hukum Pascal yang dikemukakan oleh Pascal pada 1653.

Secara analisis sederhana, Hukum Pascal dapat digambarkan seperti pada Gambar 9.

Gambar 9. Tekanan F1 di pipa satu sama besar dengan gaya angkat di pipa dua.

Tekanan oleh gaya sebesar F₁ terhadap pipa 1 yang memiliki luas penampang pipa A₁ , akan diteruskan oleh fluida menjadi gaya angkat sebesar F₂ pada pipa 2 yang memiliki luas penampang pipa A₂ dengan besar tekanan yang sama. Oleh karena itu, secara matematis Hukum Pascal ditulis sebagai berikut.

p₁ = p₂

F₁ / A₁ = F₂ / A₂ (1–8)

dengan:

F₁ = gaya pada pengisap pipa 1,

A₁ = luas penampang pengisap pipa 1,

F₂ = gaya pada pengisap pipa 2, dan

A₂ = luas penampang pengisap pipa 2.

Contoh Soal 4 :

Alat pengangkat mobil yang memiliki luas pengisap masing-masing sebesar 0,10 m² Cerdas dan 4 × 10^–4 m² digunakan untuk mengangkat mobil seberat 2 × 10⁴ N. Berapakah besar gaya yang harus diberikan pada pengisap yang kecil?

Kunci Jawaban :

Diketahui: A₁ = 4 × 10^–4 m², A₂ = 0,1 m², dan F₂ = 2 × 10⁴ N.

F₁ = 80 N.

Dengan demikian, gaya yang harus diberikan pada pengisap yang kecil adalah 80 N.

Contoh Soal 5 :

Sebuah pompa hidrolik berbentuk silinder memiliki jari-jari 4 cm dan 20 cm. Jika pengisap kecil ditekan dengan gaya 200 N, berapakah gaya yang dihasilkan pada pengisap besar?

Kunci Jawaban :

Diketahui: r₂ = 20 cm, r₁ = 4 cm, dan F₁ = 200 N.

F2 = 5.000 N

Contoh Soal 6 :

Sebuah pipa berdiameter 9 cm dialiri air berkecepatan 5 m/s, kemudian terhubung dengan pipa berdiameter 3 cm. Kecepatan air pada pipa yang berdiameter 3 cm adalah ....

a. 3 m/s

b. 9 m/s

c. 18 m/s

d. 27 m/s

e. 45 m/s Kunci Jawaban :

Hukum Pascal dimanfaatkan dalam peralatan teknik yang banyak membantu pekerjaan manusia, antara lain dongkrak hidrolik, pompa hidrolik, mesin hidrolik pengangkat mobil, mesin pres hidrolik, dan rem hidrolik. Berikut pembahasan mengenai cara kerja beberapa alat yang menggunakan prinsip Hukum Pascal.

a. Dongkrak Hidrolik

Dongkrak hidrolik merupakan salah satu aplikasi sederhana dari Hukum Pascal. Berikut ini prinsip kerja dongkrak hidrolik. Saat pengisap kecil diberi gaya tekan, gaya tersebut akan diteruskan oleh fluida (minyak) yang terdapat di dalam pompa. Akibatnya, minyak dalam dongkrak akan menghasilkan gaya angkat pada pengisap besar dan dapat mengangkat beban di atasnya.

Gambar 10. Skema dongkrak hidrolik.

b. Mesin Hidrolik Pengangkat Mobil

Mesin hidrolik pengangkat mobil ini memiliki prinsip yang sama dengan dongkrak hidrolik. Perbedaannya terletak pada perbandingan luas penampang pengisap yang digunakan. Pada mesin pengangkat mobil, perbandingan antara luas penampang kedua pengisap sangat besar sehingga gaya angkat yang dihasilkan pada pipa berpenampang besar dan dapat digunakan untuk mengangkat mobil.

Gambar 11. Mesin hidrolik pengangkat mobil. [5]

c. Rem Hidrolik

Rem hidrolik digunakan pada mobil. Ketika Anda menekan pedal rem, gaya yang Anda berikan pada pedal akan diteruskan ke silinder utama yang berisi minyak rem. Selanjutnya, minyak rem tersebut akan menekan bantalan rem yang dihubungkan pada sebuah piringan logam sehingga timbul gesekan antara bantalan rem dengan piringan logam. Gaya gesek ini akhirnya akan menghentikan putaran roda.

Gambar 12. Prinsip kerja rem hidrolik. [5]

6. Hukum Archimedes

Anda tentunya sering melihat kapal yang berlayar di laut, benda-benda yang terapung di permukaan air, atau batuan-batuan yang tenggelam di dasar sungai. Konsep terapung, melayang, atau tenggelamnya suatu benda di dalam fluida, kali pertama diteliti oleh Archimedes.

Menurut Archimedes, benda yang dicelupkan sebagian atau seluruhnya ke dalam fluida, akan mengalami gaya ke atas. Besar gaya ke atas tersebut besarnya sama dengan berat fluida yang dipindahkan oleh benda. Secara matematis, Hukum Archimedes dituliskan sebagai berikut.

F_A = ρ_fV_fg (1–9)

dengan:

F_A = gaya ke atas (N),

ρ_f = massa jenis fluida (kg/m³),

V_f = volume fluida yang dipindahkan (m³), dan

g = percepatan gravitasi (m/s³).

Berdasarkan Persamaan (1–9) dapat diketahui bahwa besarnya gaya ke atas yang dialami benda di dalam fluida bergantung pada massa jenis fluida, volume fluida yang dipindahkan, dan percepatan gravitasi Bumi.

Tokoh Fisika :

Archimedes

Archimedes. [6]

Archimedes lahir di Syracus, Romawi.Ia dikenal dan dikenang karena sejumlah hasil karyanya di bidang Fisika dan Matematika yang memberikan banyak manfaat dalam kehidupan manusia. Hasil karyanya dalam ilmu Fisika antara lain alat penaik air dan hidrostatika. Ungkapannya yang terkenal saat ia menemukan gaya ke atas yang dialami oleh benda di dalam fluida, yaitu “ ureka” sangat melekat dengan namanya. (Sumber: www.allbiographies.com)

Percobaan Fisika Sederhana 1 :

Menguji Teori Archimedes

Alat dan Bahan

Dua buah bejana yang identik
Neraca sama lengan
Neraca pegas
Beban
Air

Prosedur

Gantunglah beban pada neraca pegas.
Catatlah nilai yang ditunjukkan oleh neraca pegas sebagai berat beban tersebut.
Isilah salah satu bejana dengan air, kemudian timbanglah beban di dalam air. Catatlah angka yang ditunjukkan oleh neraca pegas sebagai berat beban di dalam air.
Bandingkanlah berat beban saat ditimbang di udara dengan berat beban saat ditimbang di dalam air. Apakah yang dapat Anda simpulkan dari kegiatan tersebut?
Letakkan kedua bejana identik ke setiap lengan neraca sama lengan.
Isilah kedua bejana identik dengan air sampai penuh. Kemudian, secara perlahan masukkan beban ke dalam salah satu bejana, sambil menampung air yang tumpah dari dalam bejana.
Amatilah posisi neraca sama lengan setelah beban berada di dalam salah satu bejana.
Hitunglah volume beban yang digunakan, kemudian bandingkan volume tersebut dengan volume air yang dipindahkan ketika beban dimasukkan ke dalam air.
Apakah yang dapat Anda simpulkan?
Diskusikanlah bersama teman kelompok dan guru Fisika Anda.

Anda telah mengetahui bahwa suatu benda yang berada di dalam fluida dapat terapung, melayang, atau tenggelam. Agar Anda dapat mengingat kembali konsep Fisika dan persamaan yang digunakan untuk menyatakan ketiga perisiwa tersebut, pelajarilah uraian berikut.

a. Terapung

Benda yang dicelupkan ke dalam fluida akan terapung jika massa jenis benda lebih kecil daripada massa jenis fluida (ρ_b < ρ_f). Massa jenis benda yang terapung dalam fluida memenuhi persamaan berikut.

(1–10)

atau

(1–11)

dengan :

V_bf = volume benda yang tercelup dalam fluida (m³),

V_b = volume benda (m³),

h_bf = tinggi benda yang tercelup dalam fluida (m),

h_b = tinggi benda (m),

ρ_b = massa jenis benda (kg/m³), dan

ρ_f = massa jenis fluida (kg/m³).

Sebuah balok kayu (ρ = 0,6 kg/m³) bermassa 60 g dan volume 100 cm³ dimasukkan ke dalam air. Ternyata, 60 cm³ kayu tenggelam sehingga volume air yang dipindahkan sebesar 60 cm³ ( 0,6 N ).

Gambar 13. Balok kayu bervolume 100 cm3 dimasukkan ke dalam air. [7]

b. Melayang

Benda yang dicelupkan ke dalam fluida akan melayang jika massa jenis benda sama dengan massa jenis fluida (ρ_b = ρ_f). Dapatkah Anda memberikan contoh benda-benda yang melayang di dalam zat cair?

c. Tenggelam

Benda yang dicelupkan ke dalam fluida akan tenggelam jika massa jenis benda lebih besar daripada massa jenis fluida (ρ_b > ρ_f). Jika benda yang dapat tenggelam dalam fluida ditimbang di dalam fluida tersebut, berat benda akan menjadi

w_bf = w – F_A (1–12)

atau

w_bf = (ρ_b – ρ_f) V_bg (1–13)

dengan:

w_bf = berat benda dalam fluida (N), dan

w = berat benda di udara (N).

Perhatikanlah Gambar 14.

Gambar 14. (a) Balok aluminium dengan volume 100 cm3 di udara. (b) Balok aluminium dengan volume 100 cm3 ditimbang di dalam air Apakah beratnya sama? [7]

Aluminium (ρ = 2,7 g/cm³) yang bermassa 270 g dan memiliki volume 100 cm³, ditimbang di udara. Berat aluminium tersebut sebesar 2,7 N. Ketika penimbangan dilakukan di dalam air, volume air yang dipindahkan adalah 100 cm³ dan menyebabkan berat air yang dipindahkan sebesar 1 N (m = ρ V dan w = mg). Dengan demikian, gaya ke atas FA yang dialami aluminium sama dengan berat air yang dipindahkan, yaitu sebesar 1 N. Berat aluminium di dalam air menjadi

w_bf = w – F_A

w_bf = 2,7 N – 1 N

w_bf = 1,7 N

Contoh Soal 7 :

Sebuah batu memiliki berat 30 N Jika ditimbang di udara. Jika batu tersebut ditimbang di dalam air beratnya = 21 N. Jika massa jenis air adalah 1 g/cm³, tentukanlah:

a. gaya ke atas yang diterima batu,

b. volume batu, dan

c. massa jenis batu tersebut.

Kunci Jawaban :

Diketahui: w = 30 N, w_bf = 21 N, dan ρ_air = 1 g/cm³.

ρ _air = 1 g/cm³ = 1.000 kg/m³

a. w_bf = w – F_A

21 N = 30 N – F_A

F_A = 9 N

b. F_A = ρ _air V _batu g

9 N = (1.000 kg/m³) (V_batu) (10 m/s²)

V_batu = 9 × 10^–4 m³

ρ _batu= 3.333,3 kg/m³.

Sebuah bola logam padat seberat 20 N diikatkan pada seutas kawat dan dicelupkan ke dalam minyak (ρ _minyak = 0,8 g/cm³). Jika massa jenis logam 5 g/cm³, berapakah tegangan kawat?

Kunci Jawaban :

Diketahui: w_bola = 20 N, ρ _minyak = 0,8 g/cm³, dan ρ_logam = 5 g/cm³.

Berdasarkan uraian gaya-gaya yang bekerja pada bola, dapat dituliskan persamaan :

T + F_A = w

T = w – F_A = w – ρ _minyak V _bola g

T = 16,8 N.

Contoh Soal 9 :

Sebuah benda memiliki volume 20 m³ dan massa jenisnya = 800 kg/m³. Jika benda tersebut dimasukkan ke dalam air yang massa jenisnya 1.000 kg/m³, tentukanlah volume benda yang berada di atas permukaan air.

Kunci Jawaban :

Diketahui: V_benda = 20 m³, ρ_benda = 800 kg/m³, dan ρ_air = 1.000 kg/m³.

Volume air yang dipindahkan = volume benda yang tercelup

F_A = ρ _air V _air-pindah g = berat benda

F_A = ρ _air V _{bagian tercelup} g = mg

ρ _air V _{bagian tercelup} = ρ _benda V _benda

(1 kg/m³) (_{Vbagian tercelup}) = (800 kg/m³) (20 m³)

V_{bagian tercelup} = 16 m³

V_muncul = 20 m³ – 16 m³ = 4 m³.

Contoh Soal 10 :

Sebuah benda dimasukkan ke dalam air. Ternyata, 25% dari volume benda terapung di atas permukaan air. Berapakah massa jenis benda tersebut?

Kunci Jawaban :

Diketahui : V_{benda terapung} = 25%.

w_benda = F_A

mg = ρ _air V _{benda tercelup} g

ρ _air V _benda g = ρ _air V _{benda tercelup} g

Catatan Fisika :

Penaik Air

Penaik air Archimedes. [6]

Penaik air ini adalah alat yang diciptakan oleh Archimedes untuk menaikkan air dari sungai atau kanal. Prinsip dasar dari alat ini adalah bidang miring yang disusun menjadi pilinan (heliks). Apabila pegangan di ujung tabung di putar, pilinan tersebut akan mengangkat air ke atas. (Sumber: Jendela Iptek, 1997)

7. Aplikasi Hukum Archimedes

Hukum Archimedes banyak diterapkan dalam kehidupan sehari-hari, di antaranya pada hidrometer, kapal laut, kapal selam, balon udara, dan galangan kapal. Berikut ini prinsip kerja alat-alat tersebut.

a. Hidrometer

Hidrometer adalah alat yang digunakan untuk mengukur massa jenis zat cair. Proses pengukuran massa jenis zat cair menggunakan hidrometer dilakukan dengan cara memasukkan hidrometer ke dalam zat cair tersebut. Angka yang ditunjukkan oleh hidrometer telah dikalibrasi sehingga akan menunjukkan nilai massa jenis zat cair yang diukur.

Hidrometer. [8]

Berikut ini prinsip kerja hidrometer.

Gaya ke atas = berat hidrometer

F_A = w_hidrometer

ρ₁ V₁ g = mg

Oleh karena volume fluida yang dipindahkan oleh hidrometer sama dengan luas tangkai hidrometer dikalikan dengan tinggi yang tercelup maka dapat dituliskan :

ρ₁ (A h₁) = m

h₁ = m / A ρ₁

dengan :

m = massa hidrometer (kg),

A = luas tangkai (m²),

h_f = tinggi hidrometer yang tercelup dalam zat cair (m), dan

ρ_f = massa jenis zat cair (kg/m³).

Hidrometer digunakan untuk memeriksa muatan akumulator mobil dengan cara membenamkan hidrometer ke dalam larutan asam akumulator. Massa jenis asam untuk muatan akumulator penuh kira-kira = 1,25 kg/m³ dan mendekati 1 kg/m³ untuk muatan akumulator kosong.

b. Kapal Laut dan Kapal Selam

Mengapa kapal yang terbuat dari baja dapat terapung di laut? Peristiwa ini berhubungan dengan gaya apung yang dihasilkan oleh kapal baja tersebut. Perhatikan Gambar 16 berikut.

Gambar 16. Kapal yang sama pada saat kosong dan penuh muatan. Volume air yang di pindahkan oleh kapal ditandai dengan tenggelamnya kapal hingga batas garis yang ditunjukkan oleh tanda panah. [9]

Balok besi yang dicelupkan ke dalam air akan tenggelam, sedangkan balok besi yang sama jika dibentuk menyerupai perahu akan terapung. Hal ini disebabkan oleh jumlah fluida yang dipindahkan besi yang berbentuk perahu lebih besar daripada jumlah fluida yang dipindahkan balok besi. Besarnya gaya angkat yang dihasilkan perahu besi sebanding dengan volume perahu yang tercelup dan volume fluida yang dipindahkannya. Apabila gaya angkat yang dihasilkan sama besar dengan berat perahu maka perahu akan terapung. Oleh karena itu, kapal baja didesain cukup lebar agar dapat memindahkan volume fluida yang sama besar dengan berat kapal itu sendiri.

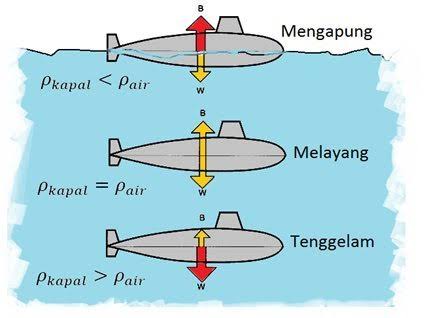
Gambar 17. Penampang kapal selam ketika (a) terapung, (b) melayang, dan (c) tenggelam.

Tahukah Anda apa yang menyebabkan kapal selam dapat terapung, melayang, dan menyelam? Kapal selam memiliki tangki pemberat di dalam lambungnya yang berfungsi mengatur kapal selam agar dapat terapung, melayang, atau tenggelam. Untuk menyelam, kapal selam mengisi tangki pemberatnya dengan air sehingga berat kapal selam akan lebih besar daripada volume air yang dipindahkannya. Akibatnya, kapal selam akan tenggelam. Sebaliknya, jika tangki pemberat terisi penuh dengan udara (air laut dipompakan keluar dari tangki pemberat), berat kapal selam akan lebih kecil daripada volume kecil yang dipindahkannya sehingga kapal selam akan terapung. Agar dapat bergerak di bawah permukaan air laut dan melayang, jumlah air laut yang dimasukkan ke dalam tangki pemberat disesuaikan dengan jumlah air laut yang dipindahkannya pada kedalaman yang diinginkan.

c. Balon Udara

Balon berisi udara panas kali pertama diterbangkan pada tanggal 21 November 1783. Udara panas dalam balon memberikan gaya angkat karena udara panas di dalam balon lebih ringan daripada udara di luar balon. Balon udara bekerja berdasarkan prinsip Hukum Archimedes. Menurut prinsip ini, dapat dinyatakan bahwa sebuah benda yang dikelilingi udara akan mengalami gaya angkat yang besarnya sama dengan volume udara yang dipindahkan oleh benda tersebut.

Gambar 18. Balon udara dapat mengambang di udara karena memanfaatkan prinsip Hukum Archimedes. [10]

8. Tegangan Permukaan

Pernahkah Anda memerhatikan bentuk cairan obat yang keluar dari penetes obat atau bentuk raksa yang diteteskan di permukaan meja? Jika Anda perhatikan, tetesan cairan obat yang keluar dari alat penetesnya berbentuk bola-bola kecil. Demikian juga dengan bentuk air raksa yang diteteskan di permukaan meja.

Tetesan zat cair atau fluida cenderung untuk memperkecil luas permukaannya. Hal tersebut terjadi karena adanya tegangan permukaan. Apakah tegangan permukaan itu? Agar dapat memahami tentang tegangan permukaan zat cair, lakukanlah kegiatan Percobaan 2. berikut.

Percobaan Fisika Sederhana 2.

Mengamati Tegangan Permukaan Zat Cair

Alat dan Bahan :

Klip kertas atau silet
Bejana
Sabun cair

Prosedur :

Gambar 19. Tegangan permukaan menyebabkan air yang jatuh pada daun membentuk permukaan sekecil mungkin. Peristiwa tersebut disebabkan adanya gaya kohesi antarmolekul air lebih besar daripada gaya adhesi antara air dan daun. [11]

Isilah bejana dengan air.
Letakkanlah klip kertas atau silet dengan perlahan-lahan di permukaan air.
Amatilah apa yang terjadi pada klip kertas atau silet tersebut.
Selanjutnya, tuangkanlah sabun cair ke dalam bejana yang berisi air dan klip kertas atau silet.
Amatilah apa yang terjadi dengan klip kertas atau silet.
Bandingkanlah hasil pengamatan Anda pada langkah 5 dengan langkah 3. Apakah yang dapat Anda simpulkan dari kegiatan tersebut?
Dapatkah Anda menjelaskan pengaruh sabun cair terhadap tegangan permukaan?
Diskusikanlah dengan teman sekelompok dan guru Fisika Anda.

Contoh tegangan permukaan yang lain dapat Anda lihat jika Anda memasukkan sebuah gelang kawat yang dipasang benang ke dalam larutan sabun. Setelah dimasukkan ke dalam larutan sabun, pada gelang kawat akan terdapat selaput tipis. Jika bagian tengah jerat benang ditusuk hingga pecah akan terlihat jerat benang yang pada mulanya berbentuk tidak beraturan, berubah menjadi berbentuk lingkaran.

Gelang kawat dan jerat benang yang dicelupkan ke dalam larutan sabun sebelum dan sesudah selaput tipis bagian tengahnya ditusuk terlihat seperti pada Gambar 20 berikut.

Gambar 20. (a) Gelang kawat dengan bentangan benang di tengahnya ketika dimasukkan ke dalam larutan sabun. (b) Setelah gelang kawat dicelupkan ke dalam larutan sabun, benang menjadi teregang dan membentuk lingkaran.

Gambar 20b menunjukkan bahwa permukaan zat cair dapat dianggap berada dalam keadaan tegang sehingga zat-zat pada kedua sisi garis saling tarik-menarik.

Tegangan permukaan (γ) di dalam selaput didefinisikan sebagai perbandingan antara gaya permukaan dan panjang permukaan yang tegak lurus gaya dan dipengaruhi oleh gaya tersebut. Perhatikan Gambar 21.

Gambar 21. Rangkaian kawat untuk mengukur tegangan permukaan selaput tipis larutan sabun. Dalam keadaan setimbang, gaya tegangan permukaan ke atas 2γ l sama dengan gaya tarik peluncur ke bawah w + T.

Gambar tersebut menunjukkan percobaan sederhana untuk melakukan pengukuran kuantitatif tentang tegangan permukaan. Seutas kawat dilengkungkan membentuk huruf U dan kawat kedua berperan sebagai peluncur yang diletakkan di ujung kawat berbentuk U. Ketika rangkaian kedua kawat tersebut dimasukkan ke dalam larutan sabun, kemudian dikeluarkan. Akibatnya, pada rangkaian kawat terbentuk selaput tipis cairan sabun. Selaput tipis tersebut akan memberikan gaya tegangan permukaan yang menarik peluncur kawat ke bagian atas kawat U (jika berat peluncur kawat sangat kecil). Ketika Anda menarik peluncur kawat ke bawah, luas permukaan selaput tipis akan membesar dan molekul-molekulnya akan bergerak dari bagian dalam cairan ke dalam lapisan permukaan.

Dalam keadaan setimbang, gaya tarik peluncur ke bawah sama dengan tegangan permukaan yang diberikan selaput tipis larutan sabun pada peluncur. Berdasarkan Gambar 21, gaya tarik peluncur ke bawah adalah

F = w + T

Jika l adalah panjang peluncur kawat maka gaya F bekerja pada panjang total 2l karena selaput tipis air sabun memiliki dua sisi permukaan. Dengan demikian, tegangan permukaan didefinisikan sebagai perbandingan antara gaya tegangan permukaan F dengan panjang d tempat gaya tersebut bekerja yang secara matematis dinyatakan dengan persamaan

γ = F d

Oleh karena d = 2l, tegangan permukaan dinyatakan dengan persamaan :

γ = F / 2l

Tegangan permukaan suatu zat cair yang bersentuhan dengan uapnya sendiri atau udara hanya bergantung pada sifat-sifat dan suhu zat cair itu. Berikut harga tegangan permukaan berdasarkan eksperimen. Berikut ini nilai tegangan permukaan beberapa zat cair berdasarkan hasil eksperimen.

Tabel 2. Harga Tegangan Permukaan Berdasarkan Eksperimen

Zat Cair yang Berhubungan dengan Udara

₁°C

Tegangan Permukaan (dyne/cm)

Air

Air sabun

Benzena

Etil Alkohol

Gliserin

Helium

Karbon Tertrakhlorida

Minyak Zaitun

Neon

Oksigen

Raksa

100

–269

–247

–193

75,6

72,8

66,2

58,9

25,0

28,9

22,3

63,1

0,12

26,8

32,0

5,15

15,7

465

Sumber: College Physics, 1980

9. Kapilaritas

Kapilaritas adalah peristiwa naik atau turunnya permukaan zat cair pada pipa kapiler, seperti yang diperlihatkan pada Gambar 22.

Gambar 22. Tabung pipa kapiler. [12]

Pada gambar tersebut, diameter dalam pipa kapiler dari kiri ke kanan semakin kecil. Semakin kecil diameter dalam pipa kapiler, kenaikan permukaan air di dalam pipa kapiler akan semakin tinggi.

Permukaan zat cair yang membasahi dinding, misalnya air, akan naik. Adapun yang tidak membasahi dinding, seperti raksa, akan turun. Dalam kehidupan sehari-hari, contoh-contoh gejala kapiler adalah sebagai berikut. Minyak tanah naik melalui sumbu lampu minyak tanah atau sumbu kompor, dinding rumah basah pada musim hujan, air tanah naik melalui pembuluh kayu.

Peristiwa air membasahi dinding, atau raksa tidak membasahi dinding dapat dijelaskan dengan memperhatikan gaya tarik-menarik antarpartikel. Gaya tarik-menarik antarpartikel sejenis disebut kohesi, sedangkan gaya tarikmenarik antarpartikel tidak sejenis disebut adhesi. Air membasahi dinding kaca karena adanya gaya kohesi antarpartikel air yang lebih kecil daripada gaya adhesi antara partikel air dan partikel dinding kaca. Sedangkan, raksa memiliki gaya kohesi lebih besar daripada gaya adhesinya dengan dinding kaca sehingga tidak membasahi dinding kaca. Gaya adhesi air yang lebih besar dari kohesinya menyebabkan permukaan air berbentuk meniskus cekung, sedangkan gaya kohesi raksa lebih besar dari gaya adhesinya sehingga menyebabkan permukaan raksa berbentuk meniskus cembung. Jika zat cair dimasukkan ke dalam suatu pipa kapiler, permukaan zat cair tersebut akan melengkung. Permukaan melengkung zat cair di dalam pipa disebut meniskus.

Gambar 23. Gaya tegangan permukaan pada fluida dalam tabung kapiler. Fluida naik jika θ < 90° dan turun jika θ > 90°.

Gambar 23 memperlihatkan gaya tegangan permukaan cairan di dalam pipa kapiler. Bentuk permukaan cairan di dalam pipa kapiler bergantung pada sudut kontak (θ ) cairan tersebut. Permukaan cairan akan naik jika θ < 90° dan turun jika θ > 90°.

Naik atau turunnya permukaan zat cair dapat ditentukan dengan persamaan berikut.

mg = F cosθ

ρ Vg = γ l cosθ

ρ π r2hg = γ 2π r cosθ

dengan:

h = kenaikan atau penurunan zat cair (m),

γ = tegangan permukaan (N/m),

g = percepatan gravitasi (m/s²), dan

r = jari-jari alas tabung/pipa (m).

Jika suatu zat cair membasahi dinding pipa, sudut kontaknya kurang dari 90° dan zat cair itu naik hingga mencapai tinggi kesetimbangan.

Gambar 24. Efek bertambah kecilnya sudut kontak yang ditimbulkan suatu zat pencemar.

Zat pencemar yang ditambahkan pada zat cair akan mengubah sudut kontak itu, misalnya detergent mengubah sudut kontak yang besarnya lebih dari 90° menjadi lebih kecil dari 90°. Sebaliknya, zat-zat yang membuat kain tahan air (waterproof) menyebabkan sudut kontak air dengan kain menjadi lebih besar dari 90°. Berikut beberapa nilai sudut kontak antara zat cair dan dinding pipa kapilernya.

Tabel 3. Sudut Kontak

Zat Cair	Dinding	Sudut Kontak
α - Bromnaftalen (C₁₀H₇Br)	Gelas Biasa Gelas Timbel Gelas Tahan Panas (Pyrex) Gelas Kuarsa	5° 6° 45' 20°30' 21°
Metilen Yodida (CH₂l₂)	Gelas Biasa Gelas Timbel Gelas Tahan Panas (Pyrex) Gelas Kuarsa	29° 30° 29° 33°
Air	Parafin	107°
Raksa	Gelas Biasa	140°

Contoh Soal 11 :

Suatu tabung berdiameter 0,4 cm jika dimasukkan secara vertikal ke dalam air, sudut kontaknya 60°. Jika tegangan permukaan air 0,5 N/m dan g = 10 m/s², tentukanlah kenaikan air pada tabung.

Kunci Jawaban :

Diketahui: d_tabung = 0,4 cm, θ = 60°, γ = 0,5 N/m, dan g = 10 m/s².

h = 0,025 m = 2,5 cm.

B. Fluida Dinamis

Pada sub bab ini Anda akan mempelajari hukum-hukum Fisika yang berlaku pada fluida bergerak (dinamis). Pada pembahasan mengenai fluida statis, Anda telah memahami bahwa hukum-hukum Fisika tentang fluida dalam keadaan statis bergantung pada massa jenis dan kedalaman titik pengamatan dari permukaan fluida. Tahukah Anda besaran-besaran yang berperan pada fluida dinamis? Untuk mengetahuinya, pelajarilah bahasan dalam subbab ini.

1. Persamaan Kontinuitas

Dalam mempelajari materi fluida dinamis, suatu fluida dianggap sebagai fluida ideal. Fluida ideal adalah fluida yang memiliki ciri-ciri berikut ini.

a. Fluida tidak dapat dimampatkan (incompressible), yaitu volume dan massa jenis fluida tidak berubah akibat tekanan yang diberikan kepadanya.

b. Fluida tidak mengalami gesekan dengan dinding tempat fluida tersebut mengalir.

c. Kecepatan aliran fluida bersifat laminer, yaitu kecepatan aliran fluida di sembarang titik berubah terhadap waktu sehingga tidak ada fluida yang memotong atau mendahului titik lainnya.

Jika lintasan sebuah titik dalam aliran fluida ideal dilukiskan, akan diperoleh suatu garis yang disebut garis aliran (streamline atau laminer flow).

Perhatikanlah Gambar 25.

Gambar 25. Setiap partikel fluida ideal mengalir menurut garis alirannya masing-masing dan tidak pernah memotong garis aliran partikel lain.

Suatu fluida ideal mengalir di dalam pipa. Setiap partikel fluida tersebut akan mengalir mengikuti garis aliran laminernya dan tidak dapat berpindah atau berpotongan dengan garis aliran yang lain.

Pada kenyataannya, Anda akan sulit menemukan fluida ideal. Sebagian besar aliran fluida di alam bersifat turbulen (turbulent flow). Garis aliran turbulen memiliki kecepatan aliran yang berbeda-beda di setiap titik. Debit aliran adalah besaran yang menunjukkan volume fluida yang mengalir melalui suatu penampang setiap satuan waktu.

Gambar 26. Kecepatan aliran fluida di pipa berpenampang besar (v1) lebih kecil daripada kecepatan aliran fluida di pipa berpenampang kecil (v2).Adapun, tekanan di pipa berpenampang besar (p1) lebih besar daripada tekanan di pipa berpenampang kecil (p2).

Secara matematis, persamaannya dituliskan sebagai berikut.

Q = v / t = Av

dengan :

V = volume fluida yang mengalir (m³),

t = waktu (s),

A = luas penampang (m²),

v = kecepatan aliran (m/s), dan

Q = debit aliran fluida (m³/s).

Untuk fluida sempurna (ideal), yaitu zat alir yang tidak dapat dimampatkan dan tidak memiliki kekentalan (viskositas), hasil kali laju aliran fluida dengan luas penampangnya selalu tetap. Secara matematis, dituliskan sebagai berikut.

A₁ v₁ = A₂ v₂ (1–18)

Persamaan 1.18 di atas disebut juga persamaan kontinuitas.

Contoh Soal 12 :

Sebuah pipa lurus memiliki dua macam penampang, masing-masing dengan luas penampang 200 mm² dan 100 mm². Pipa tersebut diletakkan secara horisontal, sedangkan air di dalamnya mengalir dari penampang besar ke penampang kecil. Jika kecepatan arus di penampang besar adalah 2 m/s, tentukanlah:

a. kecepatan arus air di penampang kecil, dan

b. volume air yang mengalir setiap menit.

Kunci Jawaban :

Diketahui: A₁ = 200 mm², A₂ = 100 mm², dan v₁ = 2 m/s.

a. A₁v₁ = A₂v₂

(200 mm²) (2 m/s) = (100 mm²)v₂

v2 = 4 m/s

Q = v / t = Av → V = Avt

Q = (200 × 10^–6 m²) (2 m/s) (60 s) = 24 × 10^–3 m³ = 2,4 × 10^–4 m³.

2. Persamaan Bernoulli

Perhatikanlah Gambar 27.

Gambar 27. Fluida bergerak dalam pipa yang ketinggian dan luas penampangnya yang berbeda. Fluida naik dari ketinggian h1 ke h2 dan kecepatannya berubah dari v1 ke v2.

Suatu fluida bergerak dari titik A yang ketinggiannya h₁ dari permukaan tanah ke titik B yang ketinggiannya h₂ dari permukaan tanah. Pada pelajaran sebelumnya, Anda telah mempelajari Hukum Kekekalan Energi Mekanik pada suatu benda. Misalnya, pada benda yang jatuh dari ketinggian tertentu dan pada anak panah yang lepas dari busurnya. Hukum Kekekalan Energi Mekanik juga berlaku pada fluida yang bergerak, seperti pada Gambar 27. Menurut penelitian Bernoulli, suatu fluida yang bergerak mengubah energinya menjadi tekanan.

Secara lengkap, Hukum Bernoulli menyatakan bahwa jumlah tekanan, energi kinetik per satuan volume, dan energi potensial per satuan volume memiliki nilai yang sama di setiap titik sepanjang aliran fluida ideal.

Persamaan matematisnya, dituliskan sebagai berikut.

p + 1/2 ρv₂ + ρgh =konstan

atau

p₁ + 1/2 ρv₁² + ρgh = p₂ + 1/2 ρv₂² + ρgh

dengan:

p = tekanan (N/m²),

v = kecepatan aliran fluida (m/s),

g = percepatan gravitasi (m/s²),

h = ketinggian pipa dari tanah (m), dan

ρ = massa jenis fluida.

3. Penerapan Persamaan Bernoulli

Hukum Bernoulli diterapkan dalam berbagai peralatan yang digunakan dalam kehidupan sehari-hari. Berikut uraian mengenai cara kerja beberapa alat yang menerapkan Hukum Bernoulli.

a. Alat Ukur Venturi

Alat ukur venturi (venturimeter) dipasang dalam suatu pipa aliran untuk mengukur laju aliran suatu zat cair. Suatu zat cair dengan massa jenis ρ mengalir melalui sebuah pipa dengan luas penampang A1 pada daerah (1). Pada daerah (2), luas penampang mengecil menjadi A2. Suatu tabung manometer (pipa U) berisi zat cair lain (raksa) dengan massa jenis ρ' dipasang pada pipa. Perhatikan Gambar 28.

Gambar 28. Penampang pipa menyempit di A2 sehingga tekanan di bagian pipa sempit lebih kecil dan fluida bergerak lebih lambat.

Kecepatan aliran zat cair di dalam pipa dapat diukur dengan persamaan.

(1–21)

Contoh Soal 13 :

Pipa venturi meter yang memiliki luas penampang masing-masing 8 × 10^–2 m² dan 5 × 10^–3 m² digunakan untuk mengukur kelajuan air. Jika beda ketinggian air raksa di dalam kedua manometer adalah 0,2 m dan g = 10 m/s², tentukanlah kelajuan air tersebut ( ρ raksa = 13.600 kg/m³).

Kunci Jawaban :

Diketahui: A₁ = 8 × 10^–2 m², A₂ = 8 × 10^–3 m², h = 0,2 m, dan g = 10 m/s².

b. Tabung Pitot (Pipa Prandtl)

Tabung pitot digunakan untuk mengukur kelajuan aliran suatu gas di dalam sebuah pipa. Perhatikanlah Gambar 29.

Gambar 29. Prinsip kerja pipa Prandtl.

Misalnya udara, mengalir melalui tabung A dengan kecepatan v. Kelajuan udara v di dalam pipa dapat ditentukan dengan persamaan :

(1–22)

c. Gaya Angkat pada Sayap Pesawat Terbang

Penampang sayap pesawat terbang memiliki bagian belakang yang lebih tajam dan sisi bagian atasnya lebih melengkung daripada sisi bagian bawahnya. Bentuk sayap tersebut menyebabkan kecepatan aliran udara bagian atas lebih besar daripada di bagian bawah sehingga tekanan udara di bawah sayap lebih besar daripada di atas sayap. Hal ini menyebabkan timbulnya daya angkat pada sayap pesawat. Agar daya angkat yang ditimbulkan pada pesawat semakin besar, sayap pesawat dimiringkan sebesar sudut tertentu terhadap arah aliran udara. Perhatikanlah Gambar 30.

Gambar 30. (a) Ketika sayap pesawat horizontal, sayap tidak mengalami gaya angkat. (b) Ketika sayap pesawat dimiringkan, pesawat mendapat gaya angkat sebesar F1 - F2.

Gaya angkat pada sayap pesawat terbang dirumuskan sebagai berikut :

F₁ – F₂ = ½ ρ A (v₂² - v₁¹) (1–23)

dengan :

F₁ – F₂ = gaya angkat pesawat terbang (N),

A = luas penampang sayap pesawat (m²),

v₁ = kecepatan udara di bagian bawah sayap (m/s),

v₂ = kecepatan udara di bagian atas sayap (m/s), dan

ρ = massa jenis fluida (udara).

Contoh Soal 14 :

Sebuah pesawat terbang bergerak dengan kecepatan tertentu sehingga udara yang melalui bagian atas dan bagian bawah sayap pesawat yang luas permukaannya 50 m² bergerak dengan kelajuan masing-masing 320 m/s dan 300 m/s. Berapakah besarnya gaya angkat pada sayap pesawat terbang tersebut? (ρ udara = 1,3 kg/m³)

Kunci Jawaban :

Diketahui: A = A = 50 m², v₂ = 320 m/s, v₁ = 300 m/s, dan ρ udara = 1,3 kg/m³.

F₁ – F₂ = 1/2 ρ A (v₂² - v₁¹)

½ (1,3 kg/m³)(50 m²)(320 m/s)² – (300 m/s)² = 403.000 N

d. Penyemprot Nyamuk

Alat penyemprot nyamuk juga bekerja berdasarkan Hukum Bernoulli. Tinjaulah alat penyemprot nyamuk pada Gambar 31.

Gambar 31. pB < pA sehingga cairan obat nyamuk di B bisa memancar keluar.

Jika pengisap dari pompa ditekan maka udara yang melewati pipa sempit pada bagian A akan memiliki kelajuan besar dan tekanan kecil. Hal tersebut menyebabkan cairan obat nyamuk yang ada pada bagian B akan naik dan ikut terdorong keluar bersama udara yang tertekan oleh pengisap pompa.

e. Kebocoran Pada Dinding Tangki

Jika air di dalam tangki mengalami kebocoran akibat adanya lubang di dinding tangki, seperti terlihat pada Gambar 32, kelajuan air yang memancar keluar dari lubang tersebut dapat dihitung berdasarkan Hukum Toricelli.

Gambar 32. Tangki dengan sebuah lubang kecil di dindingnya. Kecepatan aliran air yang keluar dari tangki sama dengan kecepatan benda yang jatuh bebas.

Menurut Hukum Toricelli, jika diameter lubang kebocoran pada dinding tangki sangat kecil dibandingkan diameter tangki, kelajuan air yang keluar dari lubang sama dengan kelajuan yang diperoleh jika air tersebut jatuh bebas dari ketinggian h. Perhatikanlah kembali Gambar 32 dengan saksama. Jarak permukaan air yang berada di dalam tangki ke lubang kebocoran dinyatakan sebagai h₁, sedangkan jarak lubang kebocoran ke dasar tangki dinyatakan h₂. Kecepatan aliran air pada saat kali pertama keluar dari lubang adalah :

Jarak horizontal tibanya air di tanah adalah :

Contoh Soal 15 :

Gambar di atas menunjukkan sebuah reservoir yang penuh dengan air. Pada dinding bagian bawah reservoir itu bocor hingga air memancar sampai di tanah. Jika g = 10 m/s², tentukanlah:

a. kecepatan air keluar dari bagian yang bocor;

b. waktu yang diperlukan air sampai ke tanah;

c. jarak pancaran maksimum di tanah diukur dari titik P.

Kunci Jawaban :

Diketahui: h₁ = 1,8 m, h₂ = 5 m, dan g = 10 m/s².

Tokoh Fisika :

Bacharuddin Jusuf Habibie

Bacharuddin Jusuf Habibie. [13]

Habibie adalah seorang putra Indonesia yang dilahirkan di Pare-Pare, Sulawesi Selatan pada tanggal 25 Juli 1936. Kecermelangannya dalam ilmu pengetahuan dan teknologi dibuktikan dengan ditemukannya Teori Habibie, Faktor Habibie, dan Metode Habibie yang diaplikasikan dalam teknologi pesawat terbang. Prestasi keilmuan Habibie ini mendapat pengakuan di dunia internasional. Ia juga berhasil menciptakan pesawat terbang pertama buatan Indonesia, yaitu CN-235 dan N-250. (Sumber: www. aist.ac.ip)

4. Viskositas

Viskositas (kekentalan) fluida menyatakan besarnya gesekan yang dialami oleh suatu fluida saat mengalir. Pada pembahasan sebelumnya, Anda telah mengetahui bahwa fluida ideal tidak memiliki viskositas. Dalam kenyataannya, fluida yang ada dalam kehidupan sehari-hari adalah fluida sejati. Oleh karena itu, bahasan mengenai viskositas hanya akan Anda temukan pada fluida sejati, yaitu fluida yang memiliki sifat-sifat sebagai berikut.

a. Dapat dimampatkan (kompresibel);

b. Mengalami gesekan saat mengalir (memiliki viskositas);

c. Alirannya turbulen.

Zat cair dan gas memiliki viskositas, hanya saja zat cair lebih kental (viscous) daripada gas. Dalam penggunaan sehari-hari, viskositas dikenal sebagai ukuran ketahanan oli untuk mengalir dalam mesin kendaraan. Viskositas oli didefinisikan dengan nomor SAE’S (Society of Automotive Engineer’s). Contoh pada sebuah pelumas tertulis

API SERVICE SJ

SAE 20W – 50

Klasifikasi service minyak pelumas ini dikembangkan oleh API (American Petroleum Institute) yang menunjukkan karakteristik service minyak pelumas dari skala terendah (SA) sampai skala tertinggi (SJ) untuk mesin-mesin berbahan bakar bensin.

Gambar 34. Aliran laminer cairan kental.

Koefisien viskositas fluida η, didefinisikan sebagai perbandingan antara tegangan luncur (F/A) dengan kecepatan perubahan regangan luncur (v/l). Secara matematis, persamaannya ditulis sebagai berikut.

atau :

Nilai viskositas setiap fluida berbeda menurut jenis material tempat fluida tersebut mengalir. Nilai viskositas beberapa fluida tertentu dapat Anda pelajari pada Tabel 2.

Tabel 4. Harga Tegangan Permukaan Berdasarkan Eksperimen

Fluida Uap Air

Viskositas

Keterangan

100°C Air 99°C

Light Machine Oil 20°C

Motor Oil SAE 10

Motor Oil SAE 20

Motor Oil SAE 30

Sirop Cokelat pada 20°C

Kecap pada 20°C

0,125 cP

0,2848 cP

102 cP

50–100 cP, 65 cP

125 cP 150–200 cP 25.000 cP

50.000 cP

Poiseuille dan Poise adalah satuan viskositas dinamis, juga disebut viskositas absolut. 1 Poiseulle (PI) = 10 Poise (P) = 1.000 cP

Sumber: people.ece.cornell.edu

Benda yang bergerak dalam fluida kental mengalami gaya gesek yang besarnya dinyatakan dengan persamaan :

Untuk benda berbentuk bola, k = 6r (perhitungan laboratorium) sehingga, diperoleh :

F_f = 6πrηv (7–27)

Persamaan (1–27) dikenal sebagai Hukum Stokes.

Jika sebuah benda berbentuk bola (kelereng) jatuh bebas dalam suatu fluida kental, kecepatannya akan bertambah karena pengaruh gravitasi Bumi hingga mencapai suatu kecepatan terbesar yang tetap. Kecepatan terbesar yang tetap tersebut dinamakan kecepatan terminal. Pada saat kecepatan terminal tercapai, berlaku keadaan

Σ F = 0

F_f + F_A= mg

F_f= mg – F_A

6π rη v_T = ρ_bv_bg – ρ_fv_bg

6π rη v_T = (ρ_b – ρ_f) V_bg

Pada benda berbentuk bola, volumenya v_b = 4/3 π r³ sehingga diperoleh persamaan :

(1–28)

dengan:

v_t = kecepatan terminal (m/s),

F_f = gaya gesek (N),

F_A = gaya ke atas (N),

ρ_b = massa jenis bola (kg/m²), dan

ρ_f= massa jenis fluida (kg/m³).

Gambar 34. Sebuah bola jatuh bebas ke dalam fluida yang memiliki viskositas tertentu.

Tokoh Fisika :

(1700–1782)

Daniel Bernoulli. [14]

Bernoulli adalah seorang ahli Fisika dan Matematika yang berasal dari Swiss. Penemuannya yang sangat terkenal adalah mengenai hidrodinamika, yaitu Hukum Bernoulli. Ia juga menemukan bahwa perilaku gas berhubungan dengan perubahan tekanan dan suhu gas tersebut. Penemuan tersebut mendasari teori kinetik gas. (Sumber: people.ece.cornell.edu)

Contoh Soal 16:

Untuk menentukan massa jenis zat cair, dibuat rangkaian alat seperti gambar di atas. Pengisap P dapat bergerak bebas dengan luas penampang 1 cm². Jika konstanta pegas = 100 N/m dan pegas tertekan sejauh 0,4 cm, massa jenis zat cair adalah ....

a. 400 kg/m³

b. 500 kg/m³

c. 750 kg/m³

d. 800 kg/m³

e. 1.000 kg/m³

Kunci Jawaban :

Pegas tertekan oleh gaya yang besarnya

F = k Δx

F = (100 N/m)(0,4 × 10^–2 m)

F = 0,4 N

Tekanan zat cair (p):

p = ρ gh

p = E/A merupakan besar tekanan zat cair yang menekan pegas, dengan F = gaya yang menekan pegas.

ρ gh = F/A

ρ = F / Agh

Rangkuman :

1. Tekanan adalah gaya yang bekerja pada suatu permukaan dibagi luas permukaan tersebut.

p = F/A (N/m² = Pascal)

2. Tekanan hidrostatis adalah tekanan yang disebabkan oleh fluida tak bergerak.

p_h = ρ gh (N/m²)

Apabila tekanan udara luar ( ρ 0) diperhitungkan, tekanan hidrostatis ditulis

p_A = p₀ + ρ gh

3. Hukum Pascal menyatakan tentang sifat fluida yang meneruskan tekanan ke segala arah sama besar.

F₁/A₁ = F₂/A₂

4. Hukum Archimedes menyatakan bahwa gaya ke atas yang dialami oleh sebuah benda dalam suatu fluida sama dengan berat fluida yang dipindahkan oleh benda tersebut.

F_A = ρ_f v_f g

5. Tegangan permukaan (γ) terjadi karena adanya gaya kohesi dan adhesi pada fluida. Secara matematis, dinyatakan dengan persamaan :

γ = F/2l

6. Kapilaritas adalah peristiwa naik atau turunnya permukaan zat cair pada pipa kapiler. Gaya kohesi dan adhesi menyebabkan timbulnya meniskus cekung atau meniskus cembung pada permukaan fluida. Persamaan kapilaritas tersebut adalah

h = 2 cosθ / ρgr

7. Fluida ideal adalah fluida yang tidak dapat dimampatkan, tidak mengalami gaya gesek ketika mengalir, dan alirannya stasioner.

8. Fluida sejati adalah fluida yang memiliki sifat dapat dimampatkan, memiliki viskositas, dan alirannya tidak stasioner (turbulen).

9. Persamaan kontinuitas menyatakan bahwa debit air

(Q) selalu tetap.

Q₁ = Q₂

A₁v₁ = A₂v₂

10. Hukum Bernoulli menyatakan bahwa tekanan, energi kinetik dan energi potensial per satuan volume fluida yang mengalir, nilainya sama di setiap titik aliran fluida.

p + ½ ρv² + ρgh = konstan

11. Viskositas (kekentalan) suatu fluida dirumuskan dalam Hukum Stokes sebagai berikut.

F =6πηr.

Anda sekarang sudah mengetahui Fluida Statis dan Fluida Dinamis. Terima kasih anda sudah berkunjung ke Perpustakaan Cyber.

Referensi : Saripudin, A., D. Rustiawan K., dan A. Suganda. 2009. Praktis Belajar Fisika 1 : untuk Kelas XI Sekolah Menengah Atas / Madrasah Aliyah Program Ilmu Pengetahuan Alam. Pusat Perbukuan Departemen Nasional, Departemen Pendidikan Nasional, Jakarta. p. 234. Referensi Lainnya : Tim Redaksi Dorling Kindersley. 1997. Jendela IPTEK, Cetakan Pertama. Jakarta: Balai Pustaka. Jones, E.R. dan Chiulders, R.L. 1994. Contemporary College Physics, Second Edition. New York: Addison Wesley Longman.

[1] http://www-math.mit.edu/~dhu/Climberweb/climberweb.html

[2] http://en.wikipedia.org/wiki/Osteichthyes [3] Halliday, David, Robert Resnick, dan Jearl Walker. 2001. Fundamentals of Physics, Sixth Edition. New York: John Wiley & Sons.

[4] http://en.wikipedia.org/wiki/Blaise_Pascal

[5] Cutnell, J. D. and K. W. Johnson. 1995. Physic. Physics, 3rd Edition. John Wiley & Sons, New York.

[6] http://en.wikipedia.org/wiki/Archimedes

[7] Microsof Encarta, 2004

[8] http://www.wilkinsonplus.com/home-brewing/wilko-hydrometer-loose-wine-and-beer/invt/0022575

[9] Hewitt, Paul G. 1993. Conceptual Physics, Eight Edition. New York: Addison Wesley Longman.

[10] http://id.wikipedia.org/wiki/Balon_udara_panas

[11] http://en.wikipedia.org/wiki/Lotus_effect [12] http://www.ctahr.hawaii.edu/mauisoil/a_comp03.aspx [13] http://id.wikipedia.org/wiki/Bacharuddin_Jusuf_Habibie [14] http://en.wikipedia.org/wiki/Daniel_Bernoulli